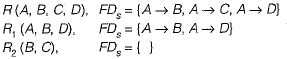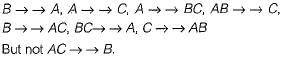Test: Functional Dependencies & Normalization- 2 - Computer Science Engineering (CSE) MCQ
15 Questions MCQ Test - Test: Functional Dependencies & Normalization- 2
A functional dependency of the form X → Y is trivial if
In an entity relationship, y is the dominant entity and x is a subordinate entity. Which of the following is/are incorrect?
Relations produced from an E-R model will always be in
Let R be a relation. Which of the following com m ents about the relation R are correct?
1. R will necessarily have a composite key if R is in BCNF but not in 4NF.
2. If R is in 3NF and if every key of R is simple , then R is in BCNF.
3. If R is in BCNF and if R has at least one
4. If R is in 3NF and if its every key is simple, then R is in 5NF.
Consider the relation:
Employee (Emp-No, Emp-name, salary, project- no, due-date)
(Assuming an 1-1 relationship between project and employees)
Project-no is functionally dependent on
Let R ( a, b, c) and S (d, e, f) be two relations in which d is the foreign key of S that refers to the primary key of R. Consider the following four operations.
1. Insert into R
2. Insert into S
3. Delete from R
4. Delete from S
Which of the following is true about the referential integrity constraint about?
Consider the following set of functional dependencies on the scheme (A, B, C).
A —> BC, B —> C, A —> B ,A B —> C
The canonical cover for this set is
Which of the following statement is false?
Given the relation R(A, B, C, D) with functional dependencies F = {A → B, A → C, A → D}, and the decomposition into relations R1(A, B, D) with functional dependencies F1 = {A → B, A → D} and R2(B, C) with functional dependencies F2 = {}, determine if the decomposition is dependency-preserving.
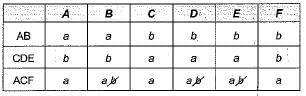
R = (A, B, C, D, E, F)
R1 - (A, B)
R2 = (C,D,E)
R3 = (A, C, F)
F= {A→B; C → DE ; AC → F;}
Does the above FD’s has lossless join property?
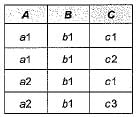
Which of the following list represents the MVDs (Mean Value Dependencies), satisfied by a relation R(A, B, C) that has the following tuples: (a1, b1, c1),(a1, b1, c2), (a2, b1, c1), (a2, b1,c3).
From the following instance of a relation schema R(A, B, C), we can conclude that:
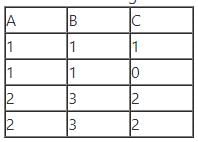
Consider the following declaration:
F: Set of functional dependencies
R: Relation of functional dependencies . R : (A, B, C, D, E)
F: (A —> BC: CD —> E; B —> D; E —> A)
Then candidate keys for R is ___________
A given relation is known to be in third normal form. Select the statement which can be inferred from this
A relation Empdtl is defined with attribute empcode (unique), name, street, city, state and pincode. For any pincode, there is only one city and state. Also, for any given street, city and state, there is just one pincode. in normalization terms, Empdtl is a relation in