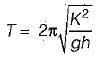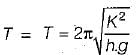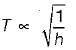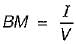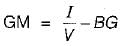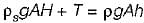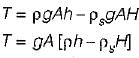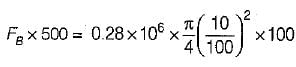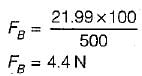Test: Buoyancy & Floatation - 2 - Mechanical Engineering MCQ
10 Questions MCQ Test Fluid Mechanics for Mechanical Engineering - Test: Buoyancy & Floatation - 2
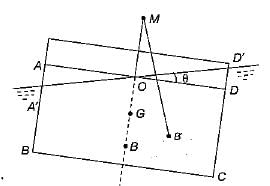
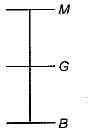
When a body, floating in a liquid is given a small angular displacement, it starts oscillating about a point known as
The time of oscillation of a floating body is given by
Where
K = Radius of Gyration of the floating body about its centre of gravity
h = Metacentric height of the floating body
Where
K = Radius of Gyration of the floating body about its centre of gravity
h = Metacentric height of the floating body
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The time of oscillation of a floating body with increase in metacentric height will be
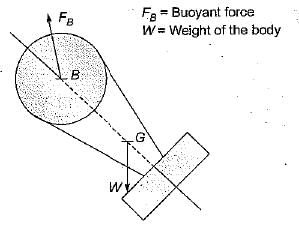
A submerged body will be in stable equillibrium. if
Which one of the following is the conditions for stable equilibrium for a floating body
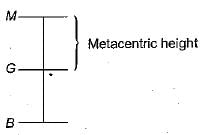
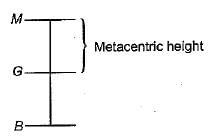
How is the metacentric height (GM) expressed
Where I = Moment of inertia of the plan of the floating body at the water surface
V = Volume of the body submerged in water
BG = Distance between the center of gravity (G) and the center of Buoyancy (B)
An odd shaped body weighing 7.5 kg and occupying 0.01 m3 volume wiil be completely submerged in a fluid having specific gravity of
A cylindrical body of cross-sectional area A height H and density ρs is immersed to a depth h in a liquid of density ρ and tied down to bottom with a string then the tension in the string is
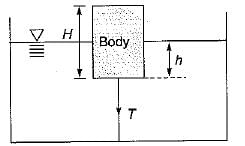
A float valve of the ‘ball-cock’ type required to close an opening of a supply pipe feeding a cistern as shown in the given figure
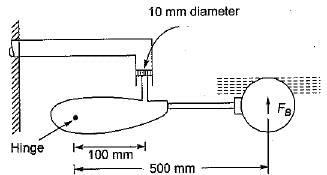
The buoyant force FB required to be exerted by the float to keep the valve closed against a pressure of 0.28 N/mm2 is
|
56 videos|104 docs|75 tests
|
|
56 videos|104 docs|75 tests
|