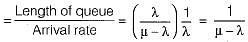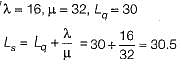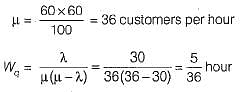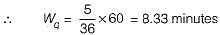Test: Queuing Theory - 1 - Mechanical Engineering MCQ
10 Questions MCQ Test Topicwise Question Bank for Mechanical Engineering - Test: Queuing Theory - 1
In queuing theory, the ratio of mean arrival rate and the mean service rate is called
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
In a queuing problem, if the arrivals are completely random, then the probability distribution of number of arrivals in a given time follows
If the number of arrival in a queue follows the poisson distribution, then the inter-arrival time obeys which one of the following distribution?
The arrival rate and the service time are usually assumed to respectively follow the
In a single server queuing model, the arrival rate is A, and the service rate is μ. What is the probability of system being idle?
In a single server queuing with arrival rate of λ and mean service time of μ, the expected number of customers in the system is 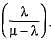
What is the expected waiting time per customer in the system?
On an average, there are 30 customers in a queue. If the arrival rate of customers into the system is 16 customers per hour and on average 32 customers leave the system per hour, then the average number of customers in the system is
A repair shop is manned by a single worker. Customers arrive at the rate of 30 per hour. Time required to provide service is exponentially distributed with mean of 100 seconds. What is the mean waiting time of a customer, needing repair facility in the queue?
In the Kendall’s notation for representing queuing models the first position represents
|
45 videos|314 tests
|
|
45 videos|314 tests
|