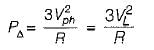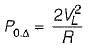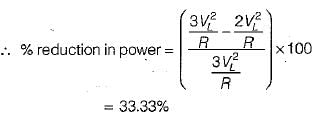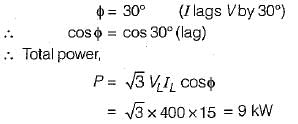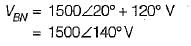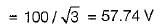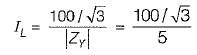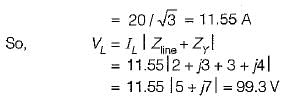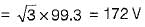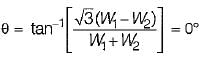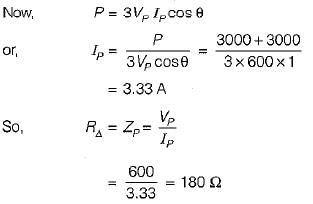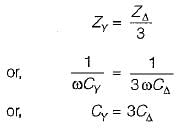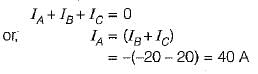All Courses
Get the App Signup / Login
Sign in Open App

Test: Poly Phase AC Circuit - 1


Test Description

10 Questions MCQ Test Topicwise Question Bank for Electrical Engineering | Test: Poly Phase AC Circuit - 1

Test: Poly Phase AC Circuit - 1 for Electrical Engineering (EE) 2023 is part of Topicwise Question Bank for Electrical Engineering preparation. The Test: Poly Phase AC Circuit - 1 questions and answers have been prepared according to the Electrical Engineering (EE) exam syllabus.The Test: Poly Phase AC Circuit - 1 MCQs are made for Electrical Engineering (EE) 2023 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: Poly Phase AC Circuit - 1 below.
Solutions of Test: Poly Phase AC Circuit - 1 questions in English are available as part of our Topicwise Question Bank for Electrical Engineering for Electrical Engineering (EE) & Test: Poly Phase AC Circuit - 1 solutions in Hindi for Topicwise Question Bank for Electrical Engineering course. Download more important topics, notes, lectures and mock test series for Electrical Engineering (EE) Exam by signing up for free. Attempt Test: Poly Phase AC Circuit - 1 | 10 questions in 30 minutes | Mock test for Electrical Engineering (EE) preparation | Free important questions MCQ to study Topicwise Question Bank for Electrical Engineering for Electrical Engineering (EE) Exam | Download free PDF with solutions
1 Crore+ students have signed up on EduRev. Have you?
Test: Poly Phase AC Circuit - 1 - Question 1
Save

Which of the following is not true for a three-phase system compared to 1-φ system?

Test: Poly Phase AC Circuit - 1 - Question 2
Save

In a balanced three-phase star connected system, the phase voltages

Detailed Solution for Test: Poly Phase AC Circuit - 1 - Question 2

Here, line-to-line voltage leads the respective phase voltage by 30°.

Test: Poly Phase AC Circuit - 1 - Question 3
Save

Three identical resistances are connected in delta against a balanced three-phase voltage supply. If one of the resistances be removed, the reduction in the power will be

Detailed Solution for Test: Poly Phase AC Circuit - 1 - Question 3

When all the resistance are present,

(Since Vph= VL for Δ connection)
When one of the phase resistance is removed,

Test: Poly Phase AC Circuit - 1 - Question 4
Save

 In a delta connected system, the line current are
Detailed Solution for Test: Poly Phase AC Circuit - 1 - Question 4

Test: Poly Phase AC Circuit - 1 - Question 5
Save

A balanced Y-connected load is supplied from a balanced 3-phase 400 V system. If the current in each phase is 15 A and lags the phase voltage by 30°, the total power will be
Detailed Solution for Test: Poly Phase AC Circuit - 1 - Question 5

Test: Poly Phase AC Circuit - 1 - Question 6
Save

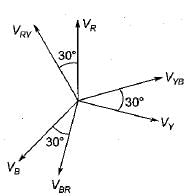
 In a balanced three-phase circuit VAN= 1500 ∠20° V and VCN = 1500 ∠-100° V.

The value of VBN will be
Detailed Solution for Test: Poly Phase AC Circuit - 1 - Question 6

Since VCN lags VAN by 120°, therefore phase sequence will be ACB.
Here, VBN will lead VAN  by 120° but, will have the same magnitude.

so,

Test: Poly Phase AC Circuit - 1 - Question 7
Save

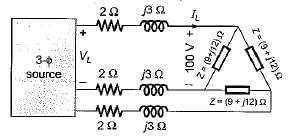
 The value of the rms line voltage VL for the below circuit if the rms line voltage is 100 V will be
Detailed Solution for Test: Poly Phase AC Circuit - 1 - Question 7

Converting the Δ-connected load in star equivalent, we have
 

So, line to neutral voltage for equivalent Y-load 

∴ Line current,

∴ Line voltage at source 

Test: Poly Phase AC Circuit - 1 - Question 8
Save

Two wattmeters, both have reading of 3 kW when connected for the two-wattmeter method with current coils in lines A and B of a 600 V ABC circuit having a balanced A load. The Δ phase impedance will be
Detailed Solution for Test: Poly Phase AC Circuit - 1 - Question 8

we have

(Since W1 = W2 = 3 kW)
or, cosθ= 1

Hence, the load will be purely resistive.

Test: Poly Phase AC Circuit - 1 - Question 9
Save

 Three capacitances, each of C/3 Farads are connected in delta. Their equivalent star value for each capacitance is
Detailed Solution for Test: Poly Phase AC Circuit - 1 - Question 9

We know that,

Test: Poly Phase AC Circuit - 1 - Question 10
Save

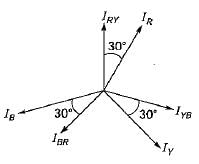
The instantaneous value of currents in both phases B and C of a 3-phase balanced system are -20 A. For a phase sequence of ABC, the instantaneous value of current in phase A is
Detailed Solution for Test: Poly Phase AC Circuit - 1 - Question 10

Since the system is balanced, therefore

Use Code STAYHOME200 and get INR 200 additional OFF
Use Coupon Code
Use Coupon Code
Information about Test: Poly Phase AC Circuit - 1 Page
In this test you can find the Exam questions for Test: Poly Phase AC Circuit - 1 solved & explained in the simplest way possible. Besides giving Questions and answers for Test: Poly Phase AC Circuit - 1, EduRev gives you an ample number of Online tests for practice
Download as PDF

Recommended Content

Recommended Tests

Download free EduRev App

Track your progress, build streaks, highlight & save important lessons and more!
© EduRev
Education Revolution
Follow Us