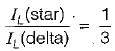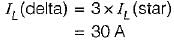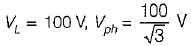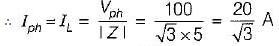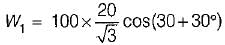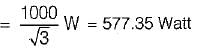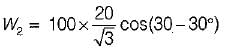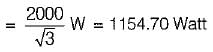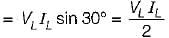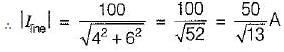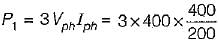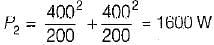Test: Poly Phase AC Circuit- 2
15 Questions MCQ Test Topicwise Question Bank for Electrical Engineering | Test: Poly Phase AC Circuit- 2
| 1 Crore+ students have signed up on EduRev. Have you? |
Three equal resistances connected in star take a line current of 10 A when fed from 400 V, 50 Hz source. If the load resistances are reconnected in delta, the line current would be
or,
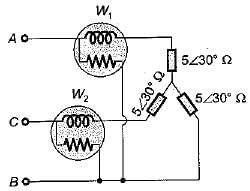
The minimum number of wattmeters required to measure the real power in an n-phase system with unbalanced load is
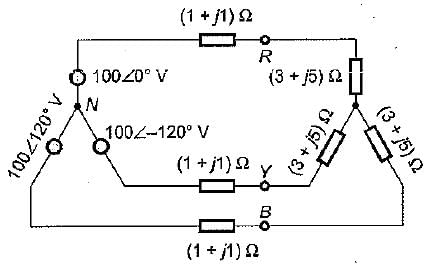
The input to the 3-phase, 50 Hz circuit shown in figure below is 100 V. For a phase sequence of ABC, the wattmeters would read
Wattmeter readings are:
W1 = VLIL cos (30 + φ)
and W2 = \/LIL cos (30 - φ)
Here,
and φ = 30°
Now,
and
Three-phase power can be measured by two-wattmeter method in case of
In the case of power measured by two-wattmeter method in a balanced 3-phase system with a pure capacitive load
W1 = VL IL cos (30° + φ)
and W2 = VL IL cos(30° - φ)
When the load is purely capacitance, then φ = - 90°.
So, W1 = VLI L cos(30°- 90°)
and W2 = VLIL cos (30° + 90°)
Hence, |W1| = |W2| but W1 = - W2
Measurement of power factor of a 3-phase system by two-wattmeter method can be obtained in case of
Two wattmeters used to measure power of a 3-phase balanced load reads W1, and W2. The reactive Dower drawn bv the load is
We know that:
(W1 - W2) = VLILsin φ = Q1 - φ
So, Q3 - φ = √3(W1 - W2)
Two wattmeters used to measure power of a 3-phase balanced load reads W1 and W2. The' reactive Dower drawn bv the load is
We know that:
(W1 - W2) = VL IL sin φ = Q1-φ
so, Q3 - φ = √3(W1 - W2)
A three-phase 220 V supply is applied to a balanced Δ-connected three phase load. The phase current being Iab =. 10∠-30°A as shown in the given figure, The total power received by the Δ-load is
Iab = 10∠-30°A
So, Ibc = 10∠-150°A
and Ica = 10∠-270° A
Phase current,
Ia = Iab - Ica = (10∠-30° - 10∠-270°) A
= 10[cos 30° - jsin 30° - cos 270° + jsin 270°]
= 10[0.866 - j0.5 - 0 - j1]
= 8.66 - j15 = 17.32 ∠-60° A
∴ Ia = 17.32 ∠-60°A
∴ Total power received
= √3 VLIL cos φL
= 3VPIP cos φph
= 3 x 220 x 10 x cos 30°
= 5715W
The magnitude of line current in the circuit shown below is
Impedance per phase
= 1 + j1 + 3 + j5
= (4 + j6) Ω
A three-phase, 400 V ac system is connected across a delta connected load having load resistance per phase of 200 Ω. If one of the phases of the delta connected load experiences an open circuit, then power consumed by the load will be
Initially, in closed - Δ, power consumed by the load is
= 2400W
Let, P2 be the power consumed in open delta.
then, 
Assertion (A): Generated voltage or current wave have no odd harmonics.
Reason (R): The field system and armature coils of the generators are all symmetrical and so generates mostly symmetrical voltage wave.
Assertion (A): RMS value of line voltage is more than √3 times of the rms value of phase voltage.
Reason (R): In a star-connected system, the line voltage contains no triple frequency harmonic content.
Assertion (A): In a balanced 3-phase star connected system, line voltages are 30° ahead of the respective phase voltages.
Reason (R): The line voltages are √3 times of the respective phase voltages,
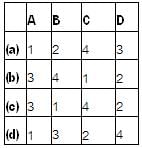
Match the List - I (Power factor) with List - II (Wattmeter readings) for the measurement of power in a three-phase system using two-wattmeter method and select the correct answer using the codes given below the lists:
List-I
A. 0.5 lag
B. Unity
C. Zero
D. 0.866
List-II
1. W1 = W2
2. W1 = 2W2
3. W1 > 0, W2 = 0
4. W1 > 0, W2 < 0
Codes:
W1 = VLIL cos (30 + φ)
and W2 = VLIL cos (30 - φ)
By finding φ from cos φ, we can find the values of W1 and W2.
|
Use Code STAYHOME200 and get INR 200 additional OFF
|
Use Coupon Code |
Download free EduRev App
Related content with Test: Poly Phase AC Circuit- 2
|
|
|
|
Related tests with Test: Poly Phase AC Circuit- 2
|
|
|
|
|
|
© EduRev
|
Education Revolution
|
Follow Us
|
