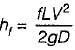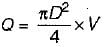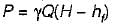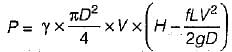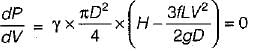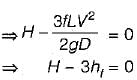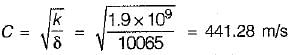Test: Flow Through Pipes - 1 - Civil Engineering (CE) MCQ
10 Questions MCQ Test Topicwise Question Bank for Civil Engineering - Test: Flow Through Pipes - 1
In a pipeline the hydraulic grade line is above the pipe centre line in the longitudinal section at a point A and below the pipe centre line at another point B. From this it can be inferred that
In a horizontal pipe of diameter D and mean velocity of flow V if Δp is the pressure difference between two sections L distance apart, then wall shear stresst ζ0 is given by
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Consider the following conditions for the pipe network shown in the given figure (Notations have the usual meaning with suffixes 1, 2 and 3 referring to respective pipes):
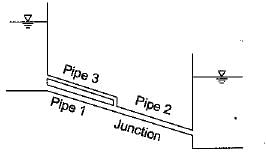
1. Q1 = Q3
2. Q2 = Q1 + Q3
3. hf1 = hf3
4. hf1 = hf2 = hf3
Which of these conditions must be satisfied by this pipe network?

1. Q1 = Q3
2. Q2 = Q1 + Q3
3. hf1 = hf3
4. hf1 = hf2 = hf3
Which of these conditions must be satisfied by this pipe network?
Maximum pressure rise due to water hammer in a pipeline (a = area of the pipe; V0 = Velocity, g = acceleration due to gravity; t = time period; L = length of the pipeline) is
Water of v = 1 centiStoke flows through a 1 cm diameter pipe. Critical flow will correspond to a discharge of approximately
A penstock is 2000 m long and the velocity of pressure wave in it is 1000 m/s. Water hammer pressure head for instantaneous closure of valve at the downstream end of the pipe is 60 m. If the valve is closed in 4 s, then what is the peak water hammer pressure in m of water?
The power transmitted through a pipeline is maximum when the head lost due to friction in the pipe is equal to
Water hammer wave velocity through a rigid pipe conveying sea water with specific weight = 10065 N/m3 and bulk modulus of elasticity = 1.96 x 109 N/m2 is