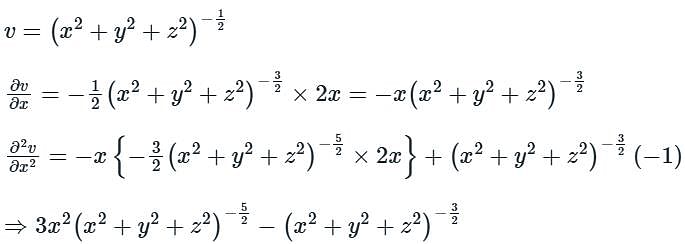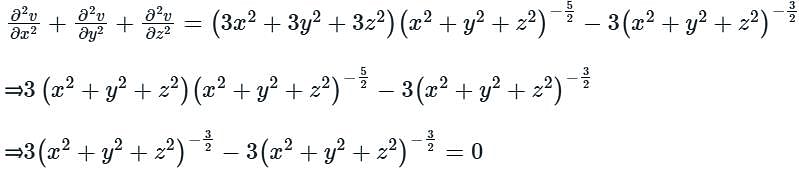Test: Partial Derivatives, Gradient- 1 - Civil Engineering (CE) MCQ
20 Questions MCQ Test Engineering Mathematics - Test: Partial Derivatives, Gradient- 1
Consider the function f(x) = x2 – x – 2. The maximum value of f(x) in the closed interval [–4, 4] is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Equation of the line normal to function f(x) = (x-8)2/3+1 at P(0,5) is
The distance between the origin and the point nearest to it on the surface z2 = 1 + xy is
Given a function
The optimal value of f(x, y)
For the function f(x) = x2e-x, the maximum occurs when x is equal to
Consider the function y = x2 – 6x + 9. The maximum value of y obtained when x varies over the interval 2 to 5 is
The magnitude of the gradient of the function f = xyz3 at (1,0,2) is
The expression curl (grad f), where f is a scalar function, is
If the velocity vector in a two – dimensional flow field is given by the vorticity vector, curl
The angle between two unit-magnitude co-planar vectors P (0.866, 0.500, 0) and Q (0.259, 0.966, 0) will be
|
65 videos|120 docs|94 tests
|
|
65 videos|120 docs|94 tests
|


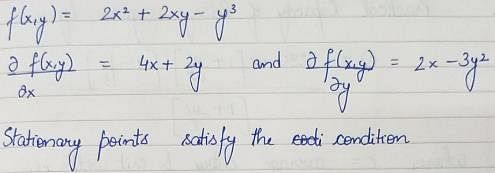

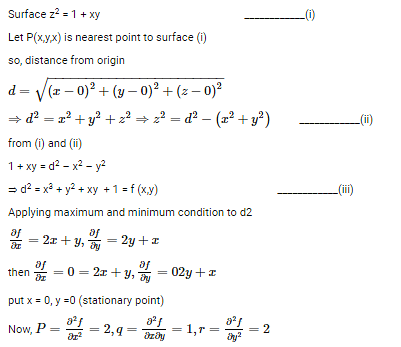

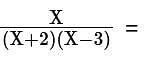
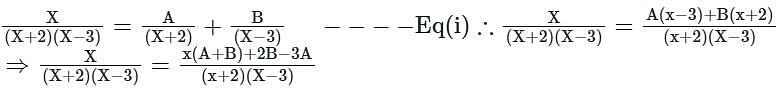
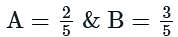
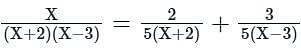
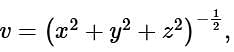 then
then 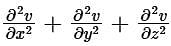 is
is