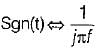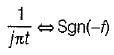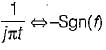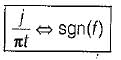Test: Continuous Time Fourier Transformer (CTFT)- 1 - Electronics and Communication Engineering (ECE) MCQ
10 Questions MCQ Test GATE ECE (Electronics) Mock Test Series 2025 - Test: Continuous Time Fourier Transformer (CTFT)- 1
If f(t) is an even function, then what is its fourier transform F (jω)?
If the fourier transform of f(t) is f(jω), then what is the fourier transform of f(-t) ?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The fourier transform of real value time signal has
The signal x(t) is a real and odd function of ‘t’ the x(ω) is
A linear system has the transfer function  When it is subjected to an input white noise process with a constant spectral dencity ‘A’ the spectral density of the output will be
When it is subjected to an input white noise process with a constant spectral dencity ‘A’ the spectral density of the output will be
The auto -correlation of a wide sense stationary random process is given by e-2|τ|. The peak valve of the spectral density is
Which one of the following is the correct fourier transform of the unit step signal?
u(t) = 1 for t > 0
= 0 for t < 0
The fourier transform of a conjugate symmetric function is always
The inverse fourier transform of sgn(f)
Fourier transform f(jω) of an arbitrary signal has the property
|
25 docs|263 tests
|
|
25 docs|263 tests
|