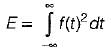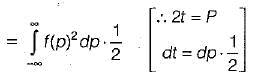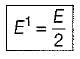Electronics and Communication Engineering (ECE) Exam > Electronics and Communication Engineering (ECE) Tests > GATE ECE (Electronics) Mock Test Series 2025 > Test: Introduction to Signals - Electronics and Communication Engineering (ECE) MCQ
Test: Introduction to Signals - Electronics and Communication Engineering (ECE) MCQ
Test Description
10 Questions MCQ Test GATE ECE (Electronics) Mock Test Series 2025 - Test: Introduction to Signals
Test: Introduction to Signals for Electronics and Communication Engineering (ECE) 2024 is part of GATE ECE (Electronics) Mock Test Series 2025 preparation. The Test: Introduction to Signals questions and answers have been
prepared according to the Electronics and Communication Engineering (ECE) exam syllabus.The Test: Introduction to Signals MCQs are made for Electronics and Communication Engineering (ECE) 2024 Exam. Find important
definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: Introduction to Signals below.
Solutions of Test: Introduction to Signals questions in English are available as part of our GATE ECE (Electronics) Mock Test Series 2025 for Electronics and Communication Engineering (ECE) & Test: Introduction to Signals solutions in
Hindi for GATE ECE (Electronics) Mock Test Series 2025 course. Download more important topics, notes, lectures and mock
test series for Electronics and Communication Engineering (ECE) Exam by signing up for free. Attempt Test: Introduction to Signals | 10 questions in 30 minutes | Mock test for Electronics and Communication Engineering (ECE) preparation | Free important questions MCQ to study GATE ECE (Electronics) Mock Test Series 2025 for Electronics and Communication Engineering (ECE) Exam | Download free PDF with solutions
Detailed Solution for Test: Introduction to Signals - Question 1
Test: Introduction to Signals - Question 2
What is the total energy of the rectangular pulse shown in figure below?
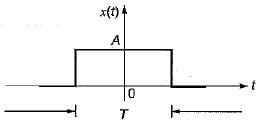

Detailed Solution for Test: Introduction to Signals - Question 2
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Detailed Solution for Test: Introduction to Signals - Question 3
Detailed Solution for Test: Introduction to Signals - Question 4
Test: Introduction to Signals - Question 5
The sampling of a function f(t) = sin(2πf0t) starts from zero-crossing. The signal can be detected, if sampling time T is:
Detailed Solution for Test: Introduction to Signals - Question 5
Test: Introduction to Signals - Question 6
What is the power and energy of the unit step sequence u(n) respectively?
Detailed Solution for Test: Introduction to Signals - Question 6
Test: Introduction to Signals - Question 7
For a periodic signal v(t) = 30 sin100t + 10 cos300t + 6 sin(500t + π/4), the
fundamental frequency in rad/s is
Detailed Solution for Test: Introduction to Signals - Question 7
Test: Introduction to Signals - Question 8
If a signal f(t) has energy ‘E’ the energy of the signal f(2t) is equal to:
Detailed Solution for Test: Introduction to Signals - Question 8
Test: Introduction to Signals - Question 9
Consider the sequence: x[n] = [- 4 - j5, 1 + j2, 4], the conjugate anti-symmetric part of the sequence is:
Detailed Solution for Test: Introduction to Signals - Question 9
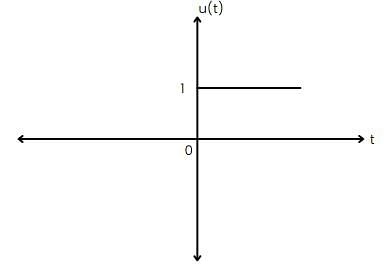
Test: Introduction to Signals - Question 10
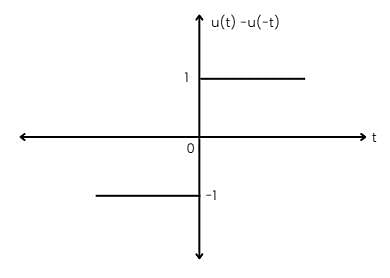
The function x(t) is shown in the figure. Even and odd parts of a unit step function u(t) are respectively:

Detailed Solution for Test: Introduction to Signals - Question 10
|
25 docs|263 tests
|
Information about Test: Introduction to Signals Page
In this test you can find the Exam questions for Test: Introduction to Signals solved & explained in the simplest way possible.
Besides giving Questions and answers for Test: Introduction to Signals, EduRev gives you an ample number of Online tests for practice
|
25 docs|263 tests
|
Download as PDF



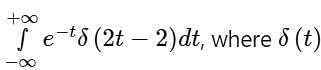 is the Dirac delta function, is
is the Dirac delta function, is


 .
.