Test: Analytical Reasoning - 2 - CAT MCQ
20 Questions MCQ Test Topic-wise Past Year Questions for CAT - Test: Analytical Reasoning - 2
Directions for Questions: Answer the questions on the basis of the information given below.
From ISBT, buses ply on 6 different routes viz. 414, 413, 427, 966, 893 and 181 at an interval of 10 min, 10 min, 12 min, 15 min, 20 min and 30 min, not necessarily in that order, to four different destinations viz. Mehrauli, Badarpur, Uttam Nagar and Azadpur. There is at least one bus for each destination. Further information is also known:
i. Two buses to the same destination cannot start at the same time.
ii. If the timings of two buses plying different routes but heading towards the same destination clash, then the bus of the route number having the shorter time interval will skip this journey.
iii. Buses on two different routes ply between ISBT and Mehrauli.
iv. The difference between the time intervals of a route to Mehrauli and Uttam Nagar is equal to the difference between the time intervals of the two routes to Uttam Nagar.
v. Buses on a route to Mehrauli leaves after every 10 min.
vi. 414 leaves for Badarpur after every 30 min.
vii. Time intervals between two different routes heading towards the same destination cannot be equal.
viii. Buses on one of the routes to Uttam Nagar leave after every 15 min.
ix. Buses to any destination can leave from ISBT with an interval of at least one minute or an integral multiple of one minute.
(2015)
Q. If 427 leaves to Mehrauli after every 10 min, then in a given hour a minimum of how many buses can ply on route 427?
From ISBT, buses ply on 6 different routes viz. 414, 413, 427, 966, 893 and 181 at an interval of 10 min, 10 min, 12 min, 15 min, 20 min and 30 min, not necessarily in that order, to four different destinations viz. Mehrauli, Badarpur, Uttam Nagar and Azadpur. There is at least one bus for each destination. Further information is also known:
i. Two buses to the same destination cannot start at the same time.
ii. If the timings of two buses plying different routes but heading towards the same destination clash, then the bus of the route number having the shorter time interval will skip this journey.
iii. Buses on two different routes ply between ISBT and Mehrauli.
iv. The difference between the time intervals of a route to Mehrauli and Uttam Nagar is equal to the difference between the time intervals of the two routes to Uttam Nagar.
v. Buses on a route to Mehrauli leaves after every 10 min.
vi. 414 leaves for Badarpur after every 30 min.
vii. Time intervals between two different routes heading towards the same destination cannot be equal.
viii. Buses on one of the routes to Uttam Nagar leave after every 15 min.
ix. Buses to any destination can leave from ISBT with an interval of at least one minute or an integral multiple of one minute.
Directions for Questions: Answer the questions on the basis of the information given below.
From ISBT, buses ply on 6 different routes viz. 414, 413, 427, 966, 893 and 181 at an interval of 10 min, 10 min, 12 min, 15 min, 20 min and 30 min, not necessarily in that order, to four different destinations viz. Mehrauli, Badarpur, Uttam Nagar and Azadpur. There is at least one bus for each destination. Further information is also known:
i. Two buses to the same destination cannot start at the same time.
ii. If the timings of two buses plying different routes but heading towards the same destination clash, then the bus of the route number having the shorter time interval will skip this journey.
iii. Buses on two different routes ply between ISBT and Mehrauli.
iv. The difference between the time intervals of a route to Mehrauli and Uttam Nagar is equal to the difference between the time intervals of the two routes to Uttam Nagar.
v. Buses on a route to Mehrauli leaves after every 10 min.
vi. 414 leaves for Badarpur after every 30 min.
vii. Time intervals between two different routes heading towards the same destination cannot be equal.
viii. Buses on one of the routes to Uttam Nagar leave after every 15 min.
ix. Buses to any destination can leave from ISBT with an interval of at least one minute or an integral multiple of one minute.
(2015)
Q. On a festival day, if frequency of all buses was increased by decreasing the time interval of all the routes by 5 min, then what can be the minimum time difference between any two buses plying to Mehrauli?
From ISBT, buses ply on 6 different routes viz. 414, 413, 427, 966, 893 and 181 at an interval of 10 min, 10 min, 12 min, 15 min, 20 min and 30 min, not necessarily in that order, to four different destinations viz. Mehrauli, Badarpur, Uttam Nagar and Azadpur. There is at least one bus for each destination. Further information is also known:
i. Two buses to the same destination cannot start at the same time.
ii. If the timings of two buses plying different routes but heading towards the same destination clash, then the bus of the route number having the shorter time interval will skip this journey.
iii. Buses on two different routes ply between ISBT and Mehrauli.
iv. The difference between the time intervals of a route to Mehrauli and Uttam Nagar is equal to the difference between the time intervals of the two routes to Uttam Nagar.
v. Buses on a route to Mehrauli leaves after every 10 min.
vi. 414 leaves for Badarpur after every 30 min.
vii. Time intervals between two different routes heading towards the same destination cannot be equal.
viii. Buses on one of the routes to Uttam Nagar leave after every 15 min.
ix. Buses to any destination can leave from ISBT with an interval of at least one minute or an integral multiple of one minute.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Directions for Questions: Answer the questions on the basis of the information given below.
From ISBT, buses ply on 6 different routes viz. 414, 413, 427, 966, 893 and 181 at an interval of 10 min, 10 min, 12 min, 15 min, 20 min and 30 min, not necessarily in that order, to four different destinations viz. Mehrauli, Badarpur, Uttam Nagar and Azadpur. There is at least one bus for each destination. Further information is also known:
i. Two buses to the same destination cannot start at the same time.
ii. If the timings of two buses plying different routes but heading towards the same destination clash, then the bus of the route number having the shorter time interval will skip this journey.
iii. Buses on two different routes ply between ISBT and Mehrauli.
iv. The difference between the time intervals of a route to Mehrauli and Uttam Nagar is equal to the difference between the time intervals of the two routes to Uttam Nagar.
v. Buses on a route to Mehrauli leaves after every 10 min.
vi. 414 leaves for Badarpur after every 30 min.
vii. Time intervals between two different routes heading towards the same destination cannot be equal.
viii. Buses on one of the routes to Uttam Nagar leave after every 15 min.
ix. Buses to any destination can leave from ISBT with an interval of at least one minute or an integral multiple of one minute.
(2015)
Q. Which of the following statements is necessarily TRUE?
From ISBT, buses ply on 6 different routes viz. 414, 413, 427, 966, 893 and 181 at an interval of 10 min, 10 min, 12 min, 15 min, 20 min and 30 min, not necessarily in that order, to four different destinations viz. Mehrauli, Badarpur, Uttam Nagar and Azadpur. There is at least one bus for each destination. Further information is also known:
i. Two buses to the same destination cannot start at the same time.
ii. If the timings of two buses plying different routes but heading towards the same destination clash, then the bus of the route number having the shorter time interval will skip this journey.
iii. Buses on two different routes ply between ISBT and Mehrauli.
iv. The difference between the time intervals of a route to Mehrauli and Uttam Nagar is equal to the difference between the time intervals of the two routes to Uttam Nagar.
v. Buses on a route to Mehrauli leaves after every 10 min.
vi. 414 leaves for Badarpur after every 30 min.
vii. Time intervals between two different routes heading towards the same destination cannot be equal.
viii. Buses on one of the routes to Uttam Nagar leave after every 15 min.
ix. Buses to any destination can leave from ISBT with an interval of at least one minute or an integral multiple of one minute.
Directions for Questions: Answer the questions on the basis of the information given below.
From ISBT, buses ply on 6 different routes viz. 414, 413, 427, 966, 893 and 181 at an interval of 10 min, 10 min, 12 min, 15 min, 20 min and 30 min, not necessarily in that order, to four different destinations viz. Mehrauli, Badarpur, Uttam Nagar and Azadpur. There is at least one bus for each destination. Further information is also known:
i. Two buses to the same destination cannot start at the same time.
ii. If the timings of two buses plying different routes but heading towards the same destination clash, then the bus of the route number having the shorter time interval will skip this journey.
iii. Buses on two different routes ply between ISBT and Mehrauli.
iv. The difference between the time intervals of a route to Mehrauli and Uttam Nagar is equal to the difference between the time intervals of the two routes to Uttam Nagar.
v. Buses on a route to Mehrauli leaves after every 10 min.
vi. 414 leaves for Badarpur after every 30 min.
vii. Time intervals between two different routes heading towards the same destination cannot be equal.
viii. Buses on one of the routes to Uttam Nagar leave after every 15 min.
ix. Buses to any destination can leave from ISBT with an interval of at least one minute or an integral multiple of one minute.
(2015)
Q. If condition (iii) is not there, then what can be the minimum difference between the time intervals between the buses plying to Uttam Nagar?
Directions for Questions: Answer the questions on the basis of the information given below.
In a given season of F1 racing, 9 races are to be held. There are 8 teams with two drivers in each team and the points are awarded to the drivers in each race as per to the following table.

Two championships viz. ‘Driver’s Championship’ and ‘Constructor’s Championship’ take place simultaneously. ‘Driver’s Championship’ is given to the player who has the maximum number of points at the end of the season. ‘Constructor’s Championship’ is given to the team for which the sum of the points of two its drivers is the maximum. A driver is said to get the podium finish only when he is among the top 3 rankers in a race. After the first 6 races, the point standings of the 16 drivers is as follows:
(2015)
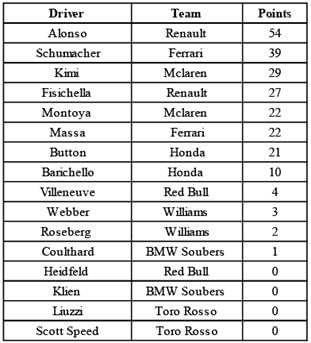
Q. If Alonso got the podium finish in each of the first 6 races, then what was the maximum number of races in which he had 2nd rank?
Directions for Questions: Answer the questions on the basis of the information given below.
In a given season of F1 racing, 9 races are to be held. There are 8 teams with two drivers in each team and the points are awarded to the drivers in each race as per to the following table.

Two championships viz. ‘Driver’s Championship’ and ‘Constructor’s Championship’ take place simultaneously. ‘Driver’s Championship’ is given to the player who has the maximum number of points at the end of the season. ‘Constructor’s Championship’ is given to the team for which the sum of the points of two its drivers is the maximum. A driver is said to get the podium finish only when he is among the top 3 rankers in a race. After the first 6 races, the point standings of the 16 drivers is as follows:
(2015)

Q. Apart from the first six races, Alonso got the podium finish in the 7th race as well. However, he was not allowed to participate in the subsequent races due to mechanical failure. At the end of the season, if Schumacher won the ‘Driver’s Championship’, then which of the following could have been his lowest rank in any of the last three races?
Directions for Questions: Answer the questions on the basis of the information given below.
In a given season of F1 racing, 9 races are to be held. There are 8 teams with two drivers in each team and the points are awarded to the drivers in each race as per to the following table.

Two championships viz. ‘Driver’s Championship’ and ‘Constructor’s Championship’ take place simultaneously. ‘Driver’s Championship’ is given to the player who has the maximum number of points at the end of the season. ‘Constructor’s Championship’ is given to the team for which the sum of the points of two its drivers is the maximum. A driver is said to get the podium finish only when he is among the top 3 rankers in a race. After the first 6 races, the point standings of the 16 drivers is as follows:
(2015)

Q. Which of the following statements CANNOT be true?
Directions for Questions: Answer the questions on the basis of the information given below.
In a given season of F1 racing, 9 races are to be held. There are 8 teams with two drivers in each team and the points are awarded to the drivers in each race as per to the following table.

Two championships viz. ‘Driver’s Championship’ and ‘Constructor’s Championship’ take place simultaneously. ‘Driver’s Championship’ is given to the player who has the maximum number of points at the end of the season. ‘Constructor’s Championship’ is given to the team for which the sum of the points of two its drivers is the maximum. A driver is said to get the podium finish only when he is among the top 3 rankers in a race. After the first 6 races, the point standings of the 16 drivers is as follows:
(2015)

Q. If Schumacher ranked 9th in one of the first six races, then which of the following CANNOT be the points scored by him in any one of the first six races?
Directions for Questions: Answer the questions on the basis of the information given below.
A group has to be selected from seven persons containing two women (Rehana and Kavya) and five men (Rohit, Rahul, Kamal, Nusarat and John). Rohit would not like to be in the group if Rahul is selected. Rahul and John want to be selected together in the group. Kavya would like to be in the group only if Kamal is also there. Kamal, if selected, would not like Nusarat in the group.
Rohit would like to be in the group only if Nusarat is also there. Kamal insists that Rehana must be selected in case he is there in the group.
(2015)
Q. Which of the following is an acceptable combination of a group of three?
Directions for Questions: Answer the questions on the basis of the information given below.
A group has to be selected from seven persons containing two women (Rehana and Kavya) and five men (Rohit, Rahul, Kamal, Nusarat and John). Rohit would not like to be in the group if Rahul is selected. Rahul and John want to be selected together in the group. Kavya would like to be in the group only if Kamal is also there. Kamal, if selected, would not like Nusarat in the group.
Rohit would like to be in the group only if Nusarat is also there. Kamal insists that Rehana must be selected in case he is there in the group.
(2015)
Q. Which of the following is an acceptable combination of a group of four?
Directions for Questions: Answer the questions on the basis of the information given below.
A group has to be selected from seven persons containing two women (Rehana and Kavya) and five men (Rohit, Rahul, Kamal, Nusarat and John). Rohit would not like to be in the group if Rahul is selected. Rahul and John want to be selected together in the group. Kavya would like to be in the group only if Kamal is also there. Kamal, if selected, would not like Nusarat in the group.
Rohit would like to be in the group only if Nusarat is also there. Kamal insists that Rehana must be selected in case he is there in the group.
(2015)
Q. Which of the following statements is true?
Directions for Questions: Answer the questions on the basis of the information given below.
A group has to be selected from seven persons containing two women (Rehana and Kavya) and five men (Rohit, Rahul, Kamal, Nusarat and John). Rohit would not like to be in the group if Rahul is selected. Rahul and John want to be selected together in the group. Kavya would like to be in the group only if Kamal is also there. Kamal, if selected, would not like Nusarat in the group.
Rohit would like to be in the group only if Nusarat is also there. Kamal insists that Rehana must be selected in case he is there in the group.
(2015)
Q. If a group of five members has to be selected, then in how many ways is it possible such that Kamal is definitely a member of the group?
Directions for Questions: Answer the questions on the basis of the information given below.
Sixteen teams – A through P – participated in the Hockey World Cup,2013. The tournament was conducted in two stages. In the first stage, the teams were divided into two groups – teams A to H in group 1 and teams I to P in group 2. In the first stage, each team in a group played exactly one match against every other team in that group. At the end of the first stage, the top four teams from each group advanced to the second stage while the rest got eliminated. The second stage comprised three rounds – Quarterfinals, Semi-finals and Finals. A round involves one match for each team. The winner of a match in a round advanced to the next round, while the loser got eliminated. The team that remains undefeated in the second stage was declared the winner of the tournament.
At the end of the first stage, top four teams in each group were determined on the basis of total number of matches won by individual teams; in case, two or more teams in a group were ended up with the same number of wins, ties were resolved by a series of complex tiebreaking rules to determine the top four positions. The teams qualifying for the second stage from group 1 were A, B, C and D and those from group 2 were I, J, K and L. No match in the tournament ended in a draw/tie.
(2015)
Q. In the tournament, if E and L won the same number of matches and L was the winner of the tournament, then what was the sum of the number of matches won by E and that by L?
Directions for Questions: Answer the questions on the basis of the information given below.
Sixteen teams – A through P – participated in the Hockey World Cup,2013. The tournament was conducted in two stages. In the first stage, the teams were divided into two groups – teams A to H in group 1 and teams I to P in group 2. In the first stage, each team in a group played exactly one match against every other team in that group. At the end of the first stage, the top four teams from each group advanced to the second stage while the rest got eliminated. The second stage comprised three rounds – Quarterfinals, Semi-finals and Finals. A round involves one match for each team. The winner of a match in a round advanced to the next round, while the loser got eliminated. The team that remains undefeated in the second stage was declared the winner of the tournament.
At the end of the first stage, top four teams in each group were determined on the basis of total number of matches won by individual teams; in case, two or more teams in a group were ended up with the same number of wins, ties were resolved by a series of complex tiebreaking rules to determine the top four positions. The teams qualifying for the second stage from group 1 were A, B, C and D and those from group 2 were I, J, K and L. No match in the tournament ended in a draw/tie.
(2015)
Q. The number of matches won in the first stage by a team that advanced to the second stage could not be less than.
Directions for Questions: Answer the questions on the basis of the information given below.
Sixteen teams – A through P – participated in the Hockey World Cup,2013. The tournament was conducted in two stages. In the first stage, the teams were divided into two groups – teams A to H in group 1 and teams I to P in group 2. In the first stage, each team in a group played exactly one match against every other team in that group. At the end of the first stage, the top four teams from each group advanced to the second stage while the rest got eliminated. The second stage comprised three rounds – Quarterfinals, Semi-finals and Finals. A round involves one match for each team. The winner of a match in a round advanced to the next round, while the loser got eliminated. The team that remains undefeated in the second stage was declared the winner of the tournament.
At the end of the first stage, top four teams in each group were determined on the basis of total number of matches won by individual teams; in case, two or more teams in a group were ended up with the same number of wins, ties were resolved by a series of complex tiebreaking rules to determine the top four positions. The teams qualifying for the second stage from group 1 were A, B, C and D and those from group 2 were I, J, K and L. No match in the tournament ended in a draw/tie.
(2015)
Q. How many of the following statements is/are true?
(i) Maximum number of teams which could have one win in the first stage was 6.
(ii) Maximum number of teams which could have three wins in the first stage was 12.
(iii) Number of teams which had exactly 2 wins in the second stage was 2.
Directions for Questions: Answer the questions on the basis of the information given below.
Sixteen teams – A through P – participated in the Hockey World Cup,2013. The tournament was conducted in two stages. In the first stage, the teams were divided into two groups – teams A to H in group 1 and teams I to P in group 2. In the first stage, each team in a group played exactly one match against every other team in that group. At the end of the first stage, the top four teams from each group advanced to the second stage while the rest got eliminated. The second stage comprised three rounds – Quarterfinals, Semi-finals and Finals. A round involves one match for each team. The winner of a match in a round advanced to the next round, while the loser got eliminated. The team that remains undefeated in the second stage was declared the winner of the tournament.
At the end of the first stage, top four teams in each group were determined on the basis of total number of matches won by individual teams; in case, two or more teams in a group were ended up with the same number of wins, ties were resolved by a series of complex tiebreaking rules to determine the top four positions. The teams qualifying for the second stage from group 1 were A, B, C and D and those from group 2 were I, J, K and L. No match in the tournament ended in a draw/tie.
(2015)
Q. The value of the total of number of matches won, in the first stage, by teams A, B, C and D together could not be more than.
Directions for Questions: Answer the questions on the basis of information given below.
Volleyball is a sport played by two teams on a playing court divided by a net.
The object of the game is to send the ball over the net in order to ground it on the opponent’s court, and to prevent the same effort by the opponent.
The team has three hits for returning the ball. The rally continues until the ball is grounded on the playing court, goes “out” or a team fails to return it properly. In Volleyball, the team winning a rally scores a point (Rally Point System).
There are six players on court in a volleyball team.
Matches are played in five sets. The first four sets are played to 25 points, with the final set being played to 15 points. A team must win a set by at least two points.
There is no ceiling, so a set continues until one of the teams gains a two-point advantage.
(2014)
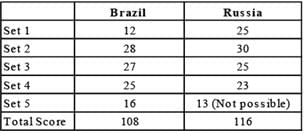
A match was played between Brazil and Russia in which
(i) Only three sets finished with the minimum threshold points.
(ii) The final score of Russia was same in two of the sets in which it won one of the sets.
(iii) In one of the sets, the final score of Brazil was less than half of Russia.
(iv) The score of Brazil in one of the sets is same as the score of Russia in one of the other set. Both of them lost their respective sets with a different margin.
(v) The total score of five sets of Brazil and Russia were 108 and 116 respectively. Also, Brazil won 3 sets.
(vi) The maximum score by any team in the five sets was 30 and the minimum was 12. Russia scored 23 points in one of the sets.
(vii) There were only three sets in which a team won by exactly two-point advantage.
Q. What was the maximum difference by which a team won the set?
Directions for Questions: Answer the questions on the basis of information given below.
Volleyball is a sport played by two teams on a playing court divided by a net.
The object of the game is to send the ball over the net in order to ground it on the opponent’s court, and to prevent the same effort by the opponent.
The team has three hits for returning the ball. The rally continues until the ball is grounded on the playing court, goes “out” or a team fails to return it properly. In Volleyball, the team winning a rally scores a point (Rally Point System).
There are six players on court in a volleyball team.
Matches are played in five sets. The first four sets are played to 25 points, with the final set being played to 15 points. A team must win a set by at least two points.
There is no ceiling, so a set continues until one of the teams gains a two-point advantage.
(2014)
A match was played between Brazil and Russia in which
(i) Only three sets finished with the minimum threshold points.
(ii) The final score of Russia was same in two of the sets in which it won one of the sets.
(iii) In one of the sets, the final score of Brazil was less than half of Russia.
(iv) The score of Brazil in one of the sets is same as the score of Russia in one of the other set. Both of them lost their respective sets with a different margin.
(v) The total score of five sets of Brazil and Russia were 108 and 116 respectively. Also, Brazil won 3 sets.
(vi) The maximum score by any team in the five sets was 30 and the minimum was 12. Russia scored 23 points in one of the sets.
(vii) There were only three sets in which a team won by exactly two-point advantage.
Q. What was the score of Russia in the fifth set?
Directions for Questions: Answer the questions on the basis of information given below.
Volleyball is a sport played by two teams on a playing court divided by a net.
The object of the game is to send the ball over the net in order to ground it on the opponent’s court, and to prevent the same effort by the opponent.
The team has three hits for returning the ball. The rally continues until the ball is grounded on the playing court, goes “out” or a team fails to return it properly. In Volleyball, the team winning a rally scores a point (Rally Point System).
There are six players on court in a volleyball team.
Matches are played in five sets. The first four sets are played to 25 points, with the final set being played to 15 points. A team must win a set by at least two points.
There is no ceiling, so a set continues until one of the teams gains a two-point advantage.
(2014)
A match was played between Brazil and Russia in which
(i) Only three sets finished with the minimum threshold points.
(ii) The final score of Russia was same in two of the sets in which it won one of the sets.
(iii) In one of the sets, the final score of Brazil was less than half of Russia.
(iv) The score of Brazil in one of the sets is same as the score of Russia in one of the other set. Both of them lost their respective sets with a different margin.
(v) The total score of five sets of Brazil and Russia were 108 and 116 respectively. Also, Brazil won 3 sets.
(vi) The maximum score by any team in the five sets was 30 and the minimum was 12. Russia scored 23 points in one of the sets.
(vii) There were only three sets in which a team won by exactly two-point advantage.
Q. In how many sets, the score of Brazil was an even number?
Directions for Questions: Answer the questions on the basis of information given below.
Volleyball is a sport played by two teams on a playing court divided by a net.
The object of the game is to send the ball over the net in order to ground it on the opponent’s court, and to prevent the same effort by the opponent.
The team has three hits for returning the ball. The rally continues until the ball is grounded on the playing court, goes “out” or a team fails to return it properly. In Volleyball, the team winning a rally scores a point (Rally Point System).
There are six players on court in a volleyball team.
Matches are played in five sets. The first four sets are played to 25 points, with the final set being played to 15 points. A team must win a set by at least two points.
There is no ceiling, so a set continues until one of the teams gains a two-point advantage.
(2014)
A match was played between Brazil and Russia in which
(i) Only three sets finished with the minimum threshold points.
(ii) The final score of Russia was same in two of the sets in which it won one of the sets.
(iii) In one of the sets, the final score of Brazil was less than half of Russia.
(iv) The score of Brazil in one of the sets is same as the score of Russia in one of the other set. Both of them lost their respective sets with a different margin.
(v) The total score of five sets of Brazil and Russia were 108 and 116 respectively. Also, Brazil won 3 sets.
(vi) The maximum score by any team in the five sets was 30 and the minimum was 12. Russia scored 23 points in one of the sets.
(vii) There were only three sets in which a team won by exactly two-point advantage.
Q. What was the score which was common with both the teams, and in which both won their respective sets?
|
43 docs|31 tests
|
|
43 docs|31 tests
|