Test: Analytical Reasoning - 3 - CAT MCQ
20 Questions MCQ Test Topic-wise Past Year Questions for CAT - Test: Analytical Reasoning - 3
Directions for Questions: Answer the questions on the basis of the information given below.
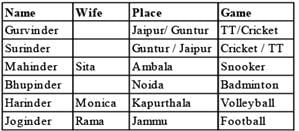
There are 6 friends — Gurvinder, Surinder, Mahinder, Bhupinder, Harinder and Joginder. Their wives are
— Sita, Rama, Dolly, Monica, Trisna and Kaveri (not in the same order as their husbands). Each of these 6 friends belong to exactly one out of Ambala, Jaipur, Guntur, Kapurthala, Noida and Jammu (not necessarily in order). Each of them plays exactly one of the games — cricket, football, volleyball, snooker, TT and badminton (again not necessarily in that order). Each of the friends is married to one lady only.
— Husbands of Dolly, Trisna or Kaveri do not play football or volleyball.
— The one who is from Guntur plays cricket.
— Joginder plays football and is from Jammu.
— Mahinder and Harinder are married to Sita and Monica respectively but are not from Guntur.
— The men from Jaipur and Kapurthala are TT and volleyball players respectively.
— Bhupinder is from Noida.
— Rama is married to the man from Jammu.
— Mahinder plays snooker.
(2014)
Q. Who is married to the man from Kapurthala?
There are 6 friends — Gurvinder, Surinder, Mahinder, Bhupinder, Harinder and Joginder. Their wives are
— Sita, Rama, Dolly, Monica, Trisna and Kaveri (not in the same order as their husbands). Each of these 6 friends belong to exactly one out of Ambala, Jaipur, Guntur, Kapurthala, Noida and Jammu (not necessarily in order). Each of them plays exactly one of the games — cricket, football, volleyball, snooker, TT and badminton (again not necessarily in that order). Each of the friends is married to one lady only.
— Husbands of Dolly, Trisna or Kaveri do not play football or volleyball.
— The one who is from Guntur plays cricket.
— Joginder plays football and is from Jammu.
— Mahinder and Harinder are married to Sita and Monica respectively but are not from Guntur.
— The men from Jaipur and Kapurthala are TT and volleyball players respectively.
— Bhupinder is from Noida.
— Rama is married to the man from Jammu.
— Mahinder plays snooker.
Directions for Questions: Answer the questions on the basis of the information given below.
There are 6 friends — Gurvinder, Surinder, Mahinder, Bhupinder, Harinder and Joginder. Their wives are
— Sita, Rama, Dolly, Monica, Trisna and Kaveri (not in the same order as their husbands). Each of these 6 friends belong to exactly one out of Ambala, Jaipur, Guntur, Kapurthala, Noida and Jammu (not necessarily in order). Each of them plays exactly one of the games — cricket, football, volleyball, snooker, TT and badminton (again not necessarily in that order). Each of the friends is married to one lady only.
— Husbands of Dolly, Trisna or Kaveri do not play football or volleyball.
— The one who is from Guntur plays cricket.
— Joginder plays football and is from Jammu.
— Mahinder and Harinder are married to Sita and Monica respectively but are not from Guntur.
— The men from Jaipur and Kapurthala are TT and volleyball players respectively.
— Bhupinder is from Noida.
— Rama is married to the man from Jammu.
— Mahinder plays snooker.
(2014)
Q. The person who plays Snooker belongs to which place?
There are 6 friends — Gurvinder, Surinder, Mahinder, Bhupinder, Harinder and Joginder. Their wives are
— Sita, Rama, Dolly, Monica, Trisna and Kaveri (not in the same order as their husbands). Each of these 6 friends belong to exactly one out of Ambala, Jaipur, Guntur, Kapurthala, Noida and Jammu (not necessarily in order). Each of them plays exactly one of the games — cricket, football, volleyball, snooker, TT and badminton (again not necessarily in that order). Each of the friends is married to one lady only.
— Husbands of Dolly, Trisna or Kaveri do not play football or volleyball.
— The one who is from Guntur plays cricket.
— Joginder plays football and is from Jammu.
— Mahinder and Harinder are married to Sita and Monica respectively but are not from Guntur.
— The men from Jaipur and Kapurthala are TT and volleyball players respectively.
— Bhupinder is from Noida.
— Rama is married to the man from Jammu.
— Mahinder plays snooker.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Directions for Questions: Answer the questions on the basis of the information given below.
There are 6 friends — Gurvinder, Surinder, Mahinder, Bhupinder, Harinder and Joginder. Their wives are
— Sita, Rama, Dolly, Monica, Trisna and Kaveri (not in the same order as their husbands). Each of these 6 friends belong to exactly one out of Ambala, Jaipur, Guntur, Kapurthala, Noida and Jammu (not necessarily in order). Each of them plays exactly one of the games — cricket, football, volleyball, snooker, TT and badminton (again not necessarily in that order). Each of the friends is married to one lady only.
— Husbands of Dolly, Trisna or Kaveri do not play football or volleyball.
— The one who is from Guntur plays cricket.
— Joginder plays football and is from Jammu.
— Mahinder and Harinder are married to Sita and Monica respectively but are not from Guntur.
— The men from Jaipur and Kapurthala are TT and volleyball players respectively.
— Bhupinder is from Noida.
— Rama is married to the man from Jammu.
— Mahinder plays snooker.
(2014)
Q. Which game is being played by Bhupinder?
There are 6 friends — Gurvinder, Surinder, Mahinder, Bhupinder, Harinder and Joginder. Their wives are
— Sita, Rama, Dolly, Monica, Trisna and Kaveri (not in the same order as their husbands). Each of these 6 friends belong to exactly one out of Ambala, Jaipur, Guntur, Kapurthala, Noida and Jammu (not necessarily in order). Each of them plays exactly one of the games — cricket, football, volleyball, snooker, TT and badminton (again not necessarily in that order). Each of the friends is married to one lady only.
— Husbands of Dolly, Trisna or Kaveri do not play football or volleyball.
— The one who is from Guntur plays cricket.
— Joginder plays football and is from Jammu.
— Mahinder and Harinder are married to Sita and Monica respectively but are not from Guntur.
— The men from Jaipur and Kapurthala are TT and volleyball players respectively.
— Bhupinder is from Noida.
— Rama is married to the man from Jammu.
— Mahinder plays snooker.
Directions for Questions: Answer the questions on the basis of the information given below.
There are 6 friends — Gurvinder, Surinder, Mahinder, Bhupinder, Harinder and Joginder. Their wives are
— Sita, Rama, Dolly, Monica, Trisna and Kaveri (not in the same order as their husbands). Each of these 6 friends belong to exactly one out of Ambala, Jaipur, Guntur, Kapurthala, Noida and Jammu (not necessarily in order). Each of them plays exactly one of the games — cricket, football, volleyball, snooker, TT and badminton (again not necessarily in that order). Each of the friends is married to one lady only.
— Husbands of Dolly, Trisna or Kaveri do not play football or volleyball.
— The one who is from Guntur plays cricket.
— Joginder plays football and is from Jammu.
— Mahinder and Harinder are married to Sita and Monica respectively but are not from Guntur.
— The men from Jaipur and Kapurthala are TT and volleyball players respectively.
— Bhupinder is from Noida.
— Rama is married to the man from Jammu.
— Mahinder plays snooker.
(2014)
Q. Who is the wife of Surinder?
Directions for Questions: Answer the questions on the basis of information given below.
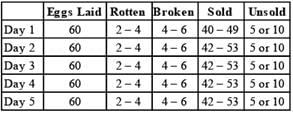
A farmer has 60 hens in his poultry farm. Each of these 60 hens lays one egg per day. On each day out of the eggs laid, some of the eggs are found to be rotten and some of the eggs get broken. Only the eggs that are neither rotten nor broken are taken to the market for sale but due to some unavoidable reasons some eggs are not sold. The eggs that are not sold are brought back to the poultry farm.
(2014)
Additional Information Given:
I. Out of the eggs that are brought back on each day, 40% are rotten and 20% are broken the next morning (and they are always integers).
II. Out of the eggs that are brought back to the poultry farm on each day, the eggs that are neither broken nor rotten are taken along with the eggs that are laid by the hens on the next day to the market for sale.
III. On any particular day the number of eggs that are not sold is less than 20% of the number of eggs that are taken to be sold out of the eggs that are laid on each day.
IV. Out of the eggs that are laid on each day, the number of eggs that are rotten is greater than 1 but less than 5 and the number of eggs that got broken is greater than 3 and less than 7.
V. Every week has five days and each week starts from day 1 and ends on day 5. Assume there are no eggs with the farmer at the beginning of day 1 of the given week.
Q. Find the minimum possible aggregate number of eggs sold on day 4 and day 5.
Directions for Questions: Answer the questions on the basis of information given below.
A farmer has 60 hens in his poultry farm. Each of these 60 hens lays one egg per day. On each day out of the eggs laid, some of the eggs are found to be rotten and some of the eggs get broken. Only the eggs that are neither rotten nor broken are taken to the market for sale but due to some unavoidable reasons some eggs are not sold. The eggs that are not sold are brought back to the poultry farm.
(2014)
Additional Information Given:
I. Out of the eggs that are brought back on each day, 40% are rotten and 20% are broken the next morning (and they are always integers).
II. Out of the eggs that are brought back to the poultry farm on each day, the eggs that are neither broken nor rotten are taken along with the eggs that are laid by the hens on the next day to the market for sale.
III. On any particular day the number of eggs that are not sold is less than 20% of the number of eggs that are taken to be sold out of the eggs that are laid on each day.
IV. Out of the eggs that are laid on each day, the number of eggs that are rotten is greater than 1 but less than 5 and the number of eggs that got broken is greater than 3 and less than 7.
V. Every week has five days and each week starts from day 1 and ends on day 5. Assume there are no eggs with the farmer at the beginning of day 1 of the given week.
Q. If the number of eggs that got rotten and broken is maximum possible in a particular week, then find the difference between the total number of eggs that got rotten and the total number of eggs that got broken across all the five days of the week.
Directions for Questions: Answer the questions on the basis of information given below.
A farmer has 60 hens in his poultry farm. Each of these 60 hens lays one egg per day. On each day out of the eggs laid, some of the eggs are found to be rotten and some of the eggs get broken. Only the eggs that are neither rotten nor broken are taken to the market for sale but due to some unavoidable reasons some eggs are not sold. The eggs that are not sold are brought back to the poultry farm.
(2014)
Additional Information Given:
I. Out of the eggs that are brought back on each day, 40% are rotten and 20% are broken the next morning (and they are always integers).
II. Out of the eggs that are brought back to the poultry farm on each day, the eggs that are neither broken nor rotten are taken along with the eggs that are laid by the hens on the next day to the market for sale.
III. On any particular day the number of eggs that are not sold is less than 20% of the number of eggs that are taken to be sold out of the eggs that are laid on each day.
IV. Out of the eggs that are laid on each day, the number of eggs that are rotten is greater than 1 but less than 5 and the number of eggs that got broken is greater than 3 and less than 7.
V. Every week has five days and each week starts from day 1 and ends on day 5. Assume there are no eggs with the farmer at the beginning of day 1 of the given week.
Q. What can be the maximum number of eggs (that are unbroken and not rotten) that were left unsold at the end of the fifth day?
Directions for Questions: Answer the questions on the basis of information given below.
A farmer has 60 hens in his poultry farm. Each of these 60 hens lays one egg per day. On each day out of the eggs laid, some of the eggs are found to be rotten and some of the eggs get broken. Only the eggs that are neither rotten nor broken are taken to the market for sale but due to some unavoidable reasons some eggs are not sold. The eggs that are not sold are brought back to the poultry farm.
(2014)
Additional Information Given:
I. Out of the eggs that are brought back on each day, 40% are rotten and 20% are broken the next morning (and they are always integers).
II. Out of the eggs that are brought back to the poultry farm on each day, the eggs that are neither broken nor rotten are taken along with the eggs that are laid by the hens on the next day to the market for sale.
III. On any particular day the number of eggs that are not sold is less than 20% of the number of eggs that are taken to be sold out of the eggs that are laid on each day.
IV. Out of the eggs that are laid on each day, the number of eggs that are rotten is greater than 1 but less than 5 and the number of eggs that got broken is greater than 3 and less than 7.
V. Every week has five days and each week starts from day 1 and ends on day 5. Assume there are no eggs with the farmer at the beginning of day 1 of the given week.
Q. If the number of eggs sold on any day of the week is maximum possible then what is the aggregate sum of the total number of eggs sold in the entire week?
Directions for Questions: Answer the questions on the basis of the information given below.
A Cricket team of 11 players is to be formed from a group of 15 players—A, B, C, D, E, F, G, H, I, J, K, L, M, N and O. Among the players A, D, K, L, M, N and O are batsmen; B, C, E, F, G and H are bowlers; I and J are wicketkeepers. It is also known that:
I. The team must have at least 5 batsmen and exactly 1 wicketkeeper.
II. H can be selected only if B is selected.
III. F can be selected only if both G and N are selected.
IV. If I is selected, then F is also selected.
V. K and M cannot be selected together for the team. The same is true for B and G.
(2013)
Q. In how many ways can the team be formed?
Directions for Questions: Answer the questions on the basis of the information given below.
A Cricket team of 11 players is to be formed from a group of 15 players—A, B, C, D, E, F, G, H, I, J, K, L, M, N and O. Among the players A, D, K, L, M, N and O are batsmen; B, C, E, F, G and H are bowlers;
I and J are wicketkeepers. It is also known that: I. The team must have at least 5 batsmen and exactly 1 wicketkeeper.
II. H can be selected only if B is selected.
III. F can be selected only if both G and N are selected.
IV. If I is selected, then F is also selected.
V. K and M cannot be selected together for the team. The same is true for B and G.
(2013)
Q. If G is one of the bowlers in the team, then who will be the wicketkeeper?
Directions for Questions: Answer the questions on the basis of the information given below.
A Cricket team of 11 players is to be formed from a group of 15 players—A, B, C, D, E, F, G, H, I, J, K, L, M, N and O. Among the players A, D, K, L, M, N and O are batsmen; B, C, E, F, G and H are bowlers; I and J are wicketkeepers. It is also known that:
I. The team must have at least 5 batsmen and exactly 1 wicketkeeper.
II. H can be selected only if B is selected.
III. F can be selected only if both G and N are selected.
IV. If I is selected, then F is also selected.
V. K and M cannot be selected together for the team. The same is true for B and G.
(2013)
Q. If H is selected, then who among the following cannot be selected in the team?
Directions for Questions: Answer the questions on the basis of the information given below.
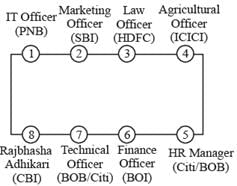
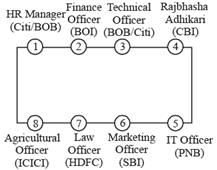
Eight persons are sitting at a rectangular table such that four persons are sitting along each of the longer sides of the table. Each person works in a different bank among PNB, SBI, HDFC, ICICI, CBI, BOB, BOI and Citi, and holds a different designation among IT Officer, Marketing Officer, Law Officer, Agricultural Officer, Rajbhasha Adhikari, Technical Officer, Finance Officer and HR Manager, not necessarily in the same order. It is also known that:
I. The Finance Officer, who works in BOI, is sitting to the immediate left of the HR Manager.
II. The Marketing Officer, who works in SBI, is sitting opposite the Technical Officer.
III. The Agricultural Officer, who works in ICICI, is sitting diagonally opposite the Rajbhasha Adhikari, who is sitting to the immediate left of the Technical Officer.
IV. The Law Officer, who works in HDFC, is sitting to the immediate left of the Marketing officer.
V. The persons who work in PNB and HDFC are sitting along the same side of the table.
VI. The Rajbhasha Adhikari, who works in CBI, is sitting at one of the extreme ends in his row.
(2013)
Q. Who is sitting to the immediate right of the Finance Officer?
Directions for Questions: Answer the questions on the basis of the information given below.
Eight persons are sitting at a rectangular table such that four persons are sitting along each of the longer sides of the table. Each person works in a different bank among PNB, SBI, HDFC, ICICI, CBI, BOB, BOI and Citi, and holds a different designation among IT Officer, Marketing Officer, Law Officer, Agricultural Officer, Rajbhasha Adhikari, Technical Officer, Finance Officer and HR Manager, not necessarily in the same order. It is also known that:
I. The Finance Officer, who works in BOI, is sitting to the immediate left of the HR Manager.
II. The Marketing Officer, who works in SBI, is sitting opposite the Technical Officer.
III. The Agricultural Officer, who works in ICICI, is sitting diagonally opposite the Rajbhasha Adhikari, who is sitting to the immediate left of the Technical Officer.
IV. The Law Officer, who works in HDFC, is sitting to the immediate left of the Marketing officer.
V. The persons who work in PNB and HDFC are sitting along the same side of the table.
VI. The Rajbhasha Adhikari, who works in CBI, is sitting at one of the extreme ends in his row.
(2013)
Q. For how many persons can we definitely determine the banks in which they work?
Directions for Questions: Answer the questions on the basis of the information given below.
Eight persons are sitting at a rectangular table such that four persons are sitting along each of the longer sides of the table. Each person works in a different bank among PNB, SBI, HDFC, ICICI, CBI, BOB, BOI and Citi, and holds a different designation among IT Officer, Marketing Officer, Law Officer, Agricultural Officer, Rajbhasha Adhikari, Technical Officer, Finance Officer and HR Manager, not necessarily in the same order. It is also known that:
I. The Finance Officer, who works in BOI, is sitting to the immediate left of the HR Manager.
II. The Marketing Officer, who works in SBI, is sitting opposite the Technical Officer.
III. The Agricultural Officer, who works in ICICI, is sitting diagonally opposite the Rajbhasha Adhikari, who is sitting to the immediate left of the Technical Officer.
IV. The Law Officer, who works in HDFC, is sitting to the immediate left of the Marketing officer.
V. The persons who work in PNB and HDFC are sitting along the same side of the table.
VI. The Rajbhasha Adhikari, who works in CBI, is sitting at one of the extreme ends in his row.
(2013)
Q. The person who is sitting opposite the Law Officer works in
Directions for Questions: Answer the questions on the basis of the information given below.
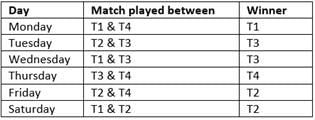
Four teams—T1, T2, T3 and T4— participated in a tournament of ‘Bat and trap’, an English bat-and-ball pub game. In the tournament, each team played exactly one match with each of the other teams. The matches were played on six consecutive days of a week from Monday to Saturday. Two points were awarded to the winner of a match and no points to the loser. No match in the tournament resulted in a tie/draw. It is also known that:
(2013)
I. T1 won only one match in the tournament and it was played on Monday.
II. The match played on Thursday was won by T4.
III. T3 won against T2 on Tuesday.
IV. T2, T3 and T4 definitely did not play on Wednesday, Monday and Saturday respectively.
V. T2 and T3 ended up with the same number of points at the end of the tournament.
Q. How many points did T4 score in the tournament?
Directions for Questions: Answer the questions on the basis of the information given below.
Four teams—T1, T2, T3 and T4— participated in a tournament of ‘Bat and trap’, an English bat-and-ball pub game. In the tournament, each team played exactly one match with each of the other teams. The matches were played on six consecutive days of a week from Monday to Saturday. Two points were awarded to the winner of a match and no points to the loser. No match in the tournament resulted in a tie/draw. It is also known that:
(2013)
I. T1 won only one match in the tournament and it was played on Monday.
II. The match played on Thursday was won by T4.
III. T3 won against T2 on Tuesday.
IV. T2, T3 and T4 definitely did not play on Wednesday, Monday and Saturday respectively.
V. T2 and T3 ended up with the same number of points at the end of the tournament.
Q. T3 lost its match against
Directions for Questions: Answer the questions on the basis of the information given below.
Four teams—T1, T2, T3 and T4— participated in a tournament of ‘Bat and trap’, an English bat-and-ball pub game. In the tournament, each team played exactly one match with each of the other teams. The matches were played on six consecutive days of a week from Monday to Saturday. Two points were awarded to the winner of a match and no points to the loser. No match in the tournament resulted in a tie/draw. It is also known that:
(2013)
I. T1 won only one match in the tournament and it was played on Monday.
II. The match played on Thursday was won by T4.
III. T3 won against T2 on Tuesday.
IV. T2, T3 and T4 definitely did not play on Wednesday, Monday and Saturday respectively.
V. T2 and T3 ended up with the same number of points at the end of the tournament.
Q. The match played on Friday was between
Directions for Questions: Answer the questions on the basis of the information given below.
Five friends, viz. Ashok, Amit, Ajay, Akansh and Abhishek are living in five different cities named Kunnamangalam, Joka, Vastrapur, Banerghatta and Prabandhnagar, not necessarily in that order. Their salaries are 700000, 800000, 900000, 1100000, 1300000 (INR per annum), in no particular order. Further, the following information is given about them:
(2012)
I. Akansh, who does not live in Banerghatta, earns a salary that is a prime number multiple of 100000.
II. Amit made a call to one of his four mentioned friends who lives in Prabandhnagar and earning a perfect square multiple of 100000 INR in salary.
III. Ajay’s salary is 100000 INR more than the average salary of Akansh and Ashok
IV. Amit lives in the city, which has the shortest name amongst the above cities.
Q. If Akansh lives in Vastrapur, then what is the average salary of the persons living in Banerghatta and Kunnamangalam?
Directions for Questions: Answer the questions on the basis of the information given below.
Five friends, viz. Ashok, Amit, Ajay, Akansh and Abhishek are living in five different cities named Kunnamangalam, Joka, Vastrapur, Banerghatta and Prabandhnagar, not necessarily in that order. Their salaries are 700000, 800000, 900000, 1100000, 1300000 (INR per annum), in no particular order. Further, the following information is given about them:
(2012)
I. Akansh, who does not live in Banerghatta, earns a salary that is a prime number multiple of 100000.
II. Amit made a call to one of his four mentioned friends who lives in Prabandhnagar and earning a perfect square multiple of 100000 INR in salary.
III. Ajay’s salary is 100000 INR more than the average salary of Akansh and Ashok
IV. Amit lives in the city, which has the shortest name amongst the above cities.
Q. Who stays in Prabandhnagar?
Directions for Questions: Answer the questions on the basis of the information given below.
Five friends, viz. Ashok, Amit, Ajay, Akansh and Abhishek are living in five different cities named Kunnamangalam, Joka, Vastrapur, Banerghatta and Prabandhnagar, not necessarily in that order. Their salaries are 700000, 800000, 900000, 1100000, 1300000 (INR per annum), in no particular order. Further, the following information is given about them:
(2012)
I. Akansh, who does not live in Banerghatta, earns a salary that is a prime number multiple of 100000.
II. Amit made a call to one of his four mentioned friends who lives in Prabandhnagar and earning a perfect square multiple of 100000 INR in salary.
III. Ajay’s salary is 100000 INR more than the average salary of Akansh and Ashok
IV. Amit lives in the city, which has the shortest name amongst the above cities.
Q. If Amit and Ajay live in cities with names starting with consecutive alphabets, then who lives in Vastrapur?
|
43 docs|31 tests
|
|
43 docs|31 tests
|