Test: Data Tabulation & Caselets - 1 - CAT MCQ
20 Questions MCQ Test Topic-wise Past Year Questions for CAT - Test: Data Tabulation & Caselets - 1
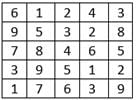
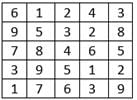
Directions for Questions: In a square layout of size 5m × 5m, 25 equal-sized square platforms of different heights are built.
The height (in metres) of individual platforms are as shown below:
(2017)
Individuals (all of same height) are seated on these platforms. We say an individual A can reach an individual B if all the three following conditions are met:
(i) A and B are in the same row or column
(ii) A is at a lower height than B
(iii) If there is/are any individual(s) between A and B, such individual(s) must be at a height lower than that of A.
Thus in the table given above, consider the individual seated at height 8 on 3rd row and 2nd column. He can be reached by four individuals. He can be reached by the individual on his left at height 7, by the two individuals on his right at heights of 4 and 6 and by the individual above at height 5.
Rows in the layout are numbered from top to bottom and columns are numbered from left to right.
Q. How many individuals in this layout can be reached by just one individual?
The height (in metres) of individual platforms are as shown below:

Individuals (all of same height) are seated on these platforms. We say an individual A can reach an individual B if all the three following conditions are met:
(i) A and B are in the same row or column
(ii) A is at a lower height than B
(iii) If there is/are any individual(s) between A and B, such individual(s) must be at a height lower than that of A.
Thus in the table given above, consider the individual seated at height 8 on 3rd row and 2nd column. He can be reached by four individuals. He can be reached by the individual on his left at height 7, by the two individuals on his right at heights of 4 and 6 and by the individual above at height 5.
Rows in the layout are numbered from top to bottom and columns are numbered from left to right.
Directions for Questions: In a square layout of size 5m × 5m, 25 equal-sized square platforms of different heights are built.
The height (in metres) of individual platforms are as shown below:
(2017)

Individuals (all of same height) are seated on these platforms. We say an individual A can reach an individual B if all the three following conditions are met:
(i) A and B are in the same row or column
(ii) A is at a lower height than B
(iii) If there is/are any individual(s) between A and B, such individual(s) must be at a height lower than that of A.
Thus in the table given above, consider the individual seated at height 8 on 3rd row and 2nd column. He can be reached by four individuals. He can be reached by the individual on his left at height 7, by the two individuals on his right at heights of 4 and 6 and by the individual above at height 5.
Rows in the layout are numbered from top to bottom and columns are numbered from left to right.
Q. Which of the following is true for any individual at a platform of height 1 m in this layout?
The height (in metres) of individual platforms are as shown below:

Individuals (all of same height) are seated on these platforms. We say an individual A can reach an individual B if all the three following conditions are met:
(i) A and B are in the same row or column
(ii) A is at a lower height than B
(iii) If there is/are any individual(s) between A and B, such individual(s) must be at a height lower than that of A.
Thus in the table given above, consider the individual seated at height 8 on 3rd row and 2nd column. He can be reached by four individuals. He can be reached by the individual on his left at height 7, by the two individuals on his right at heights of 4 and 6 and by the individual above at height 5.
Rows in the layout are numbered from top to bottom and columns are numbered from left to right.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Directions for Questions: In a square layout of size 5m × 5m, 25 equal-sized square platforms of different heights are built.
The height (in metres) of individual platforms are as shown below:
(2017)

Individuals (all of same height) are seated on these platforms. We say an individual A can reach an individual B if all the three following conditions are met:
(i) A and B are in the same row or column
(ii) A is at a lower height than B
(iii) If there is/are any individual(s) between A and B, such individual(s) must be at a height lower than that of A.
Thus in the table given above, consider the individual seated at height 8 on 3rd row and 2nd column. He can be reached by four individuals. He can be reached by the individual on his left at height 7, by the two individuals on his right at heights of 4 and 6 and by the individual above at height 5.
Rows in the layout are numbered from top to bottom and columns are numbered from left to right.
Q. We can find two individuals who cannot be reached by anyone in
The height (in metres) of individual platforms are as shown below:

Individuals (all of same height) are seated on these platforms. We say an individual A can reach an individual B if all the three following conditions are met:
(i) A and B are in the same row or column
(ii) A is at a lower height than B
(iii) If there is/are any individual(s) between A and B, such individual(s) must be at a height lower than that of A.
Thus in the table given above, consider the individual seated at height 8 on 3rd row and 2nd column. He can be reached by four individuals. He can be reached by the individual on his left at height 7, by the two individuals on his right at heights of 4 and 6 and by the individual above at height 5.
Rows in the layout are numbered from top to bottom and columns are numbered from left to right.
Directions for Questions: In a square layout of size 5m × 5m, 25 equal-sized square platforms of different heights are built.
The height (in metres) of individual platforms are as shown below:
(2017)

Individuals (all of same height) are seated on these platforms. We say an individual A can reach an individual B if all the three following conditions are met:
(i) A and B are in the same row or column
(ii) A is at a lower height than B
(iii) If there is/are any individual(s) between A and B, such individual(s) must be at a height lower than that of A.
Thus in the table given above, consider the individual seated at height 8 on 3rd row and 2nd column. He can be reached by four individuals. He can be reached by the individual on his left at height 7, by the two individuals on his right at heights of 4 and 6 and by the individual above at height 5.
Rows in the layout are numbered from top to bottom and columns are numbered from left to right.
Q. Which of the following statements is true about this layout?
Directions for Questions:
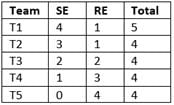
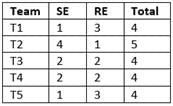
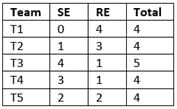
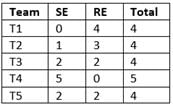
There are 21 employees working in a division, out of whom 10 are special-skilled employees (SE) and the remaining are regular skilled employees (RE). During the next five months, the division has to complete five projects every month. Out of the 25 projects, 5 projects are "challenging", while the remaining ones are "standard". Each of the challenging projects has to be completed in different months. Every month, five teams T1, T2, T3, T4 and T5, work on one project each. T1, T2, T3, T4 and T5 are allotted the challenging project in the first, second, third fourth and fifth month, respectively. The team assigned the challenging project has one more employee than the rest.
In the first month, T1 has one more SE than T2, T2 has one more SE than T3, T3 has one more SE than T4, and T4 has one more SE than T5. Between two successive months, the composition of the teams changes as follows.
(a) The team allotted the challenging project, gets two SE from the team which was allotted the challenging project in the previous month. In exchange. one RE is shifted from the former team to the latter team.
(b) After the above exchange, if T1 has any SE and T5 has any RE, then one SE is shifted from T1 to T5, and one RE is shifted from T5 to T1. Also, if T2 has any SE and T4 has any RE, then one SE is shifted from T2 to T4, and one RE is shifted from T4 to T2.
Each standard project has a total of 100 credit points, while each challenging project has 200 credit points. The credit points are equally shared between the employees included in that team.
(2017)
Q. The number of times in which the composition of team T2 and the number of times in which composition of team T4 remained unchanged in two successive months are.
Directions for Questions:
There are 21 employees working in a division, out of whom 10 are special-skilled employees (SE) and the remaining are regular skilled employees (RE). During the next five months, the division has to complete five projects every month. Out of the 25 projects, 5 projects are "challenging", while the remaining ones are "standard". Each of the challenging projects has to be completed in different months. Every month, five teams T1, T2, T3, T4 and T5, work on one project each. T1, T2, T3, T4 and T5 are allotted the challenging project in the first, second, third fourth and fifth month, respectively. The team assigned the challenging project has one more employee than the rest.
In the first month, T1 has one more SE than T2, T2 has one more SE than T3, T3 has one more SE than T4, and T4 has one more SE than T5. Between two successive months, the composition of the teams changes as follows.
(a) The team allotted the challenging project, gets two SE from the team which was allotted the challenging project in the previous month. In exchange. one RE is shifted from the former team to the latter team.
(b) After the above exchange, if T1 has any SE and T5 has any RE, then one SE is shifted from T1 to T5, and one RE is shifted from T5 to T1. Also, if T2 has any SE and T4 has any RE, then one SE is shifted from T2 to T4, and one RE is shifted from T4 to T2.
Each standard project has a total of 100 credit points, while each challenging project has 200 credit points. The credit points are equally shared between the employees included in that team.
(2017)
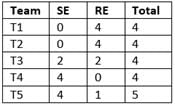
Q. The number of SE in T1 and T5 for the projects in the third month are, respectively.
Directions for Questions:
There are 21 employees working in a division, out of whom 10 are special-skilled employees (SE) and the remaining are regular skilled employees (RE). During the next five months, the division has to complete five projects every month. Out of the 25 projects, 5 projects are "challenging", while the remaining ones are "standard". Each of the challenging projects has to be completed in different months. Every month, five teams T1, T2, T3, T4 and T5, work on one project each. T1, T2, T3, T4 and T5 are allotted the challenging project in the first, second, third fourth and fifth month, respectively. The team assigned the challenging project has one more employee than the rest.
In the first month, T1 has one more SE than T2, T2 has one more SE than T3, T3 has one more SE than T4, and T4 has one more SE than T5. Between two successive months, the composition of the teams changes as follows.
(a) The team allotted the challenging project, gets two SE from the team which was allotted the challenging project in the previous month. In exchange. one RE is shifted from the former team to the latter team.
(b) After the above exchange, if T1 has any SE and T5 has any RE, then one SE is shifted from T1 to T5, and one RE is shifted from T5 to T1. Also, if T2 has any SE and T4 has any RE, then one SE is shifted from T2 to T4, and one RE is shifted from T4 to T2.
Each standard project has a total of 100 credit points, while each challenging project has 200 credit points. The credit points are equally shared between the employees included in that team.
(2017)
Q. Which of the following CANNOT be the total credit points earned by any employee from the projects?
Directions for Questions:
There are 21 employees working in a division, out of whom 10 are special-skilled employees (SE) and the remaining are regularskilled employees (RE). During the next five months, the division has to complete five projects every month. Out of the 25 projects, 5 projects are "challenging", while the remaining ones are "standard". Each of the challenging projects has to be completed in different months. Every month, five teams T1, T2, T3, T4 and T5, work on one project each. T1, T2, T3, T4 and T5 are allotted the challenging project in the first, second, third fourth and fifth month, respectively. The team assigned the challenging project has one more employee than the rest.
In the first month, T1 has one more SE than T2, T2 has one more SE than T3, T3 has one more SE than T4, and T4 has one more SE than T5. Between two successive months, the composition of the teams changes as follows.
(a) The team allotted the challenging project, gets two SE from the team which was allotted the challenging project in the previous month. In exchange. one RE is shifted from the former team to the latter team.
(b) After the above exchange, if T1 has any SE and T5 has any RE, then one SE is shifted from T1 to T5, and one RE is shifted from T5 to T1. Also, if T2 has any SE and T4 has any RE, then one SE is shifted from T2 to T4, and one RE is shifted from T4 to T2.
Each standard project has a total of 100 credit points, while each challenging project has 200 credit points. The credit points are equally shared between the employees included in that team.
(2017)
Q. One of the employees named Aneek scored 185 points. Which of the following CANNOT be true?
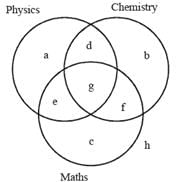
Directions for Questions: Applicants for the doctoral programmes of Ambi Institute of Engineering (AIE) and Bambi Institute of Engineering (BIE) have to appear for a Common Entrance Test (CET). The test has three sections. Physics (P), Chemistry (C), and Maths (M). Among those appearing for CET, those at or above the 80th percentile in at least two sections, and at or above the 90th percentile overall, are selected for Advanced Entrance Test (AET) conducted by AIE. AET is used by AIE for final selection.
For the 200 condidates who are at or above the 90th percentile overall based on CET, the following are known about their performance in CET.
(2017)
(a) No one is below the 80th percentile in all 3 sections.
(b) 150 are at or above the 80th percentile in exactly two sections.
(c) The number of candidates at or above the 80th percentile only in P is the same as the number of candidates at or above the 80th percentile only in C. The same is the number of candidates at or above the 80th percentile only in M.
(d) Number of candidates below 80th percentile in P. Number of candidates below 80th percentile in C. Number of candidates below 80th percentile in M = 4:2:1.
BIE uses a different process for selection. If any candidate is appearing in the AET by AIE, BIE considers their AET score for final selection provided the candidate is at or above the 80th percentile in P. Any other candidate at or above the 80th percentile in P in CET, but who is not eligible for the AET, is required to appear in a separate test to be conducted by BIE for being considered for final selection. Altogether, there are 400 candidates this year who are at or above the 80th percentile in P.
Q. What best can be concluded about the number of candidates sitting for the separate test for BIE who were at or above the 90th percentile overall in CET?
Directions for Questions: Applicants for the doctoral programmes of Ambi Institute of Engineering (AIE) and Bambi Institute of Engineering (BIE) have to appear for a Common Entrance Test (CET). The test has three sections. Physics (P), Chemistry (C), and Maths (M). Among those appearing for CET, those at or above the 80th percentile in at least two sections, and at or above the 90th percentile overall, are selected for Advanced Entrance Test (AET) conducted by AIE. AET is used by AIE for final selection.
For the 200 condidates who are at or above the 90th percentile overall based on CET, the following are known about their performance in CET.
(2017)
(a) No one is below the 80th percentile in all 3 sections.
(b) 150 are at or above the 80th percentile in exactly two sections.
(c) The number of candidates at or above the 80th percentile only in P is the same as the number of candidates at or above the 80th percentile only in C. The same is the number of candidates at or above the 80th percentile only in M.
(d) Number of candidates below 80th percentile in P. Number of candidates below 80th percentile in C. Number of candidates below 80th percentile in M = 4:2:1.
BIE uses a different process for selection. If any candidate is appearing in the AET by AIE, BIE considers their AET score for final selection provided the candidate is at or above the 80th percentile in P. Any other candidate at or above the 80th percentile in P in CET, but who is not eligible for the AET, is required to appear in a separate test to be conducted by BIE for being considered for final selection. Altogether, there are 400 candidates this year who are at or above the 80th percentile in P.
Q. If the number of candidates who are at or above the 90th percentile overall and also at or above the 80th percentile in all three sections in CET is actually a multiple of 5, what is the number of candidates who are at or above the 90th percentile overall and at or above the 80th percentile in both P and M in CET?
Directions for Questions: Applicants for the doctoral programmes of Ambi Institute of Engineering (AIE) and Bambi Institute of Engineering (BIE) have to appear for a Common Entrance Test (CET). The test has three sections. Physics (P), Chemistry (C), and Maths (M). Among those appearing for CET, those at or above the 80th percentile in at least two sections, and at or above the 90th percentile overall, are selected for Advanced Entrance Test (AET) conducted by AIE. AET is used by AIE for final selection.
For the 200 condidates who are at or above the 90th percentile overall based on CET, the following are known about their performance in CET.
(2017)
(a) No one is below the 80th percentile in all 3 sections.
(b) 150 are at or above the 80th percentile in exactly two sections.
(c) The number of candidates at or above the 80th percentile only in P is the same as the number of candidates at or above the 80th percentile only in C. The same is the number of candidates at or above the 80th percentile only in M.
(d) Number of candidates below 80th percentile in P. Number of candidates below 80th percentile in C. Number of candidates below 80th percentile in M = 4:2:1.
BIE uses a different process for selection. If any candidate is appearing in the AET by AIE, BIE considers their AET score for final selection provided the candidate is at or above the 80th percentile in P. Any other candidate at or above the 80th percentile in P in CET, but who is not eligible for the AET, is required to appear in a separate test to be conducted by BIE for being considered for final selection. Altogether, there are 400 candidates this year who are at or above the 80th percentile in P.
Q. If the number of candidates who are at or above the 90th percentile overall and also at or above the 80th percentile in all three sections in CET is actually a multiple of 5, then how many candidates were shortlisted for the AET for AIE?
Directions for Questions: Applicants for the doctoral programmes of Ambi Institute of Engineering (AIE) and Bambi Institute of Engineering (BIE) have to appear for a Common Entrance Test (CET). The test has three sections. Physics (P), Chemistry (C), and Maths (M). Among those appearing for CET, those at or above the 80th percentile in at least two sections, and at or above the 90th percentile overall, are selected for Advanced Entrance Test (AET) conducted by AIE. AET is used by AIE for final selection.
For the 200 condidates who are at or above the 90th percentile overall based on CET, the following are known about their performance in CET.
(2017)
(a) No one is below the 80th percentile in all 3 sections.
(b) 150 are at or above the 80th percentile in exactly two sections.
(c) The number of candidates at or above the 80th percentile only in P is the same as the number of candidates at or above the 80th percentile only in C. The same is the number of candidates at or above the 80th percentile only in M.
(d) Number of candidates below 80th percentile in P. Number of candidates below 80th percentile in C. Number of candidates below 80th percentile in M = 4:2:1.
BIE uses a different process for selection. If any candidate is appearing in the AET by AIE, BIE considers their AET score for final selection provided the candidate is at or above the 80th percentile in P. Any other candidate at or above the 80th percentile in P in CET, but who is not eligible for the AET, is required to appear in a separate test to be conducted by BIE for being considered for final selection. Altogether, there are 400 candidates this year who are at or above the 80th percentile in P.
Q. If the number of candidates who are at or above the 90th percentile overall and also are at or above the 80th percentile in P in CET, is more that 100, how many candidates had to sit for the separate test for BIE?
Directions for Questions:
A study to look at the early learning of rural kids was carried out in a number of villages spanning three states, chosen from the North East (NE), the West (W) and the South(S). 50 four-year old kids each were sampled from each of the 150 villages from NE, 250 villages from W and 200 villages from S. It was found that of the 30000 surveyed kids 55% studied in primary schools run by government (G), 37% in private schools (P) while the remaining 8% did not go to school (O). The kids surveyed were further divided into two groups based on whether their mothers dropped out of school before completing primary education or not. The table below gives the number of kids in different types of schools for mothers who dropped out of school before completing primary education:
(2017)
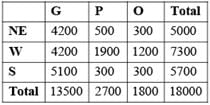
It is also known that:
(I) In S, 60% of the surveyed kids were in G. Moreover, in S, all surveyed kids whose mothers had completed primary education were in school.
(II) In NE, among the O kids, 50% had mothers who had dropped out before completing primary education.
(III) The number of kids in G in NE was the same as the number of kids in G in W.
Q. What percentage of kids from S were studying in P?
Directions for Questions:
A study to look at the early learning of rural kids was carried out in a number of villages spanning three states, chosen from the North East (NE), the West (W) and the South(S). 50 four-year old kids each were sampled from each of the 150 villages from NE, 250 villages from W and 200 villages from S. It was found that of the 30000 surveyed kids 55% studied in primary schools run by government (G), 37% in private schools (P) while the remaining 8% did not go to school (O). The kids surveyed were further divided into two groups based on whether their mothers dropped out of school before completing primary education or not. The table below gives the number of kids in different types of schools for mothers who dropped out of school before completing primary education:
(2017)

It is also known that:
(I) In S, 60% of the surveyed kids were in G. Moreover, in S, all surveyed kids whose mothers had completed primary education were in school.
(II) In NE, among the O kids, 50% had mothers who had dropped out before completing primary education.
(III) The number of kids in G in NE was the same as the number of kids in G in W.
Q. Among the kids in W whose mothers had completed primary education, how many were not in school?
Directions for Questions:
A study to look at the early learning of rural kids was carried out in a number of villages spanning three states, chosen from the North East (NE), the West (W) and the South(S). 50 four-year old kids each were sampled from each of the 150 villages from NE, 250 villages from W and 200 villages from S. It was found that of the 30000 surveyed kids 55% studied in primary schools run by government (G), 37% in private schools (P) while the remaining 8% did not go to school (O). The kids surveyed were further divided into two groups based on whether their mothers dropped out of school before completing primary education or not. The table below gives the number of kids in different types of schools for mothers who dropped out of school before completing primary education:
(2017)

It is also known that:
(I) In S, 60% of the surveyed kids were in G. Moreover, in S, all surveyed kids whose mothers had completed primary education were in school.
(II) In NE, among the O kids, 50% had mothers who had dropped out before completing primary education.
(III) The number of kids in G in NE was the same as the number of kids in G in W.
Q. In a follow up survey of the same kids two years later, it was found that all the kids were now in school. Of the kids who were not in school earlier, in one region, 25% were in G now, whereas the rest were enrolled in P, in the second region, all such kids were in G now, while in the third region, 50% of such kids has now joined G while the rest had joined P. As a result, in all three regions put together, 50% of the kids who were earlier out of school had joined G. It was also seen that no surveyed kid had changed schools.
What number of the surveyed kids now were in G in W?
Directions for Questions:
A study to look at the early learning of rural kids was carried out in a number of villages spanning three states, chosen from the North East (NE), the West (W) and the South(S). 50 four-year old kids each were sampled from each of the 150 villages from NE, 250 villages from W and 200 villages from S. It was found that of the 30000 surveyed kids 55% studied in primary schools run by government (G), 37% in private schools (P) while the remaining 8% did not go to school (O). The kids surveyed were further divided into two groups based on whether their mothers dropped out of school before completing primary education or not. The table below gives the number of kids in different types of schools for mothers who dropped out of school before completing primary education:
(2017)

It is also known that:
(I) In S, 60% of the surveyed kids were in G. Moreover, in S, all surveyed kids whose mothers had completed primary education were in school.
(II) In NE, among the O kids, 50% had mothers who had dropped out before completing primary education.
(III) The number of kids in G in NE was the same as the number of kids in G in W.
Q. In a follow up survey of the same kids two years later, it was found that all the kids were now in school. Of the kids who were not in school earlier, in one region, 25% were in G now, whereas the rest were enrolled in P, in the second region, all such kids were in G now, while in the third region, 50% of such kids had now joined G while the rest had joined P. As a result, in all three regions put together, 50% of the kids who were earlier out of school had joined G. It was also seen that no surveyed kid had changed schools.
What percentage of the surveyed kids in S, whose mothers had dropped out before completing primary education, were in G now?
Directions for Questions:
Healthy Bites is a fast food joint serving three items; burgers, fries and ice cream. It has two employees Anish and Bani who prepare the items ordered by the clients. Preparation time is 10 minutes for a burger and 2 minutes for an order of ice cream. An employee can prepare only one of these items at a time. The fries are prepared in an automatic fryer which can prepare up to 3 portions of fries at a time, and takes 5 minutes irrespective of the number of portions. The fryer does not need an employee to constantly attend to it, and we can ignore the time taken by an employee to start and stop the fryer; thus, an employee can be engaged in preparing other items while the frying is on. However fries cannot be prepared in anticipation of future orders.
Healthy Bites wishes to serve the orders as early as possible. The individual items in any order are served as and when ready; however, the order is considered to be completely served only when all the items of that order are served.
The table below gives the orders of three clients and the times at which they placed their orders:
(2017)

Q. Assume that only one client’s order can be processed at any given point of time. So, Anish or Bani cannot start preparing a new order while a previous order is being prepared.
At what time is the order placed by Client 1 completely served?
Directions for Questions:
Healthy Bites is a fast food joint serving three items; burgers, fries and ice cream. It has two employees Anish and Bani who prepare the items ordered by the clients. Preparation time is 10 minutes for a burger and 2 minutes for an order of ice cream. An employee can prepare only one of these items at a time. The fries are prepared in an automatic fryer which can prepare up to 3 portions of fries at a time, and takes 5 minutes irrespective of the number of portions. The fryer does not need an employee to constantly attend to it, and we can ignore the time taken by an employee to start and stop the fryer; thus, an employee can be engaged in preparing other items while the frying is on. However fries cannot be prepared in anticipation of future orders.
Healthy Bites wishes to serve the orders as early as possible. The individual items in any order are served as and when ready; however, the order is considered to be completely served only when all the items of that order are served.
The table below gives the orders of three clients and the times at which they placed their orders:
(2017)

Q. Assume that only one client’s order can be processed at any given point of time. So, Anish or Bani cannot start preparing a new order while a previous order is being prepared.
At what time is the order placed by Client 3 completely served?
Directions for Questions:
Healthy Bites is a fast food joint serving three items; burgers, fries and ice cream. It has two employees Anish and Bani who prepare the items ordered by the clients. Preparation time is 10 minutes for a burger and 2 minutes for an order of ice cream. An employee can prepare only one of these items at a time. The fries are prepared in an automatic fryer which can prepare up to 3 portions of fries at a time, and takes 5 minutes irrespective of the number of portions. The fryer does not need an employee to constantly attend to it, and we can ignore the time taken by an employee to start and stop the fryer; thus, an employee can be engaged in preparing other items while the frying is on. However fries cannot be prepared in anticipation of future orders.
Healthy Bites wishes to serve the orders as early as possible. The individual items in any order are served as and when ready; however, the order is considered to be completely served only when all the items of that order are served.
The table below gives the orders of three clients and the times at which they placed their orders:
(2017)

Q. Suppose the employees are allowed to process multiple orders at a time, but the preference would be to finish orders of clients who placed their orders earlier.
At what time is the order placed by Client 2 completely served?
Directions for Questions:
Healthy Bites is a fast food joint serving three items; burgers, fries and ice cream. It has two employees Anish and Bani who prepare the items ordered by the clients. Preparation time is 10 minutes for a burger and 2 minutes for an order of ice cream. An employee can prepare only one of these items at a time. The fries are prepared in an automatic fryer which can prepare up to 3 portions of fries at a time, and takes 5 minutes irrespective of the number of portions. The fryer does not need an employee to constantly attend to it, and we can ignore the time taken by an employee to start and stop the fryer; thus, an employee can be engaged in preparing other items while the frying is on. However fries cannot be prepared in anticipation of future orders.
Healthy Bites wishes to serve the orders as early as possible. The individual items in any order are served as and when ready; however, the order is considered to be completely served only when all the items of that order are served.
The table below gives the orders of three clients and the times at which they placed their orders:
(2017)

Q. Suppose the employees are allowed to process multiple orders at a time, but the preference would be to finish orders of clients who placed their orders earlier.
Also assume that the fourth client came in only at 10 : 35. Between 10: 00 and 10 : 30, for how many minutes is exactly one of the employees idle?
|
43 docs|31 tests
|
|
43 docs|31 tests
|