Test: Analysis of Stress & Strain Level - 3 - Mechanical Engineering MCQ
20 Questions MCQ Test Strength of Materials (SOM) - Test: Analysis of Stress & Strain Level - 3
On an aluminium sample, strain readings were recorded on 3-element delta rosette as follows. ε0° = −100 μs, ε120° = −500 μs and ε60° = +600 μs Then the maximum tensile strain is __________ μs.
If a small concrete cube is submerged deep in still water in such a way that the pressure exerted on all faces of the cube is P, then the maximum shear stress developed inside the cube is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Which point on the stress strain curve occurs after yield plateau?
Two wooden joists 50mm and 100mm are glued together along the joist AB as shown. Determine the normal and tangential stress in the glue if P = 200 kN
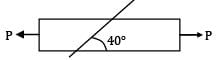
In a strained material the normal stress on one plane is 10t/cm2 tensile and the shear stress is 5t/cm2. On a plane perpendicular to this plane there is only shear stress. The center for Mohr’s circle
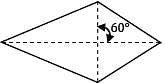
In a material under a state of plane strain, a square centered at a point gets deformed as shown in figure.
Find the shear strain γxy

Assuming E = 160 GPa and G = 100 GPa for a material, a strain tensor is given as
![]()
The shear stress, τxy is
n a strained material, normal stresses on two mutually perpendicular planes are σx and σy (both alike) accompanied by a shear stress τxy, one of the principal stresses will be zero, only if,
For which one of the following stress conditions the diameter of Mohr’s stress circle is zero?
Where σ1 =major principal stress,
σ2 = Minor principal stress and
q = Shear stress
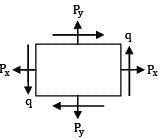
If Normal stresses of same nature px and py and shear stress q is acting on two perpendicular planes and q = (pxpy)1/2, then the major and minor principal stresses respectively are
A tensile specimen with 12 mm initial diameter and 50 mm initial length is subjected to a load of 90 kN. After sometime, the diameter is 10mm. Assuming it as in compressible material, calculate true strain along the length. (Give answer upto 3 decimal places)
A square plate of side 4 units undergoes deformation. The angle between the diagonals becomes 60°. Calculate τ45° (4 decimal places)
A square plate of side 4 units experiences the following strain components.
ϵx = 0.001
ϵy = 0.002
τxy = 0.003
Find the elongation of the diagonal (4 decimal places)
For which of the following cases distortion energy theory is more liberal when compared to shear stress theory.
I. σ1 , σ2 are equal and are tensile in nature.
II. σ1 , σ2 are equal and are compressive in nature.
III. σ1 is compressive and σ2 is tensile and the magnitudes are the same.
IV. σ1 is tensile and σ2 is compressive and the magnitudes are same
Following stress Tensor represents tri-axial state of stress at a point. Determine strain energy per unit volume in kJ/m3 .
Consider, Poisson’s ratio = 0.3 and Young’s modulus of elasticity = 200 GPa
τ = 
Following stress Tensor represents tri-axial state of stress at a point. Determine the distortion energy per unit volume in terms of kJ/m3 . Take μ = 0.3, E = 200 GPa
[σ] = 
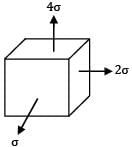
Consider the below shown loading conditions, which one will fail first according to principal strain energy theory [μ = 0.3]
I.

II.
Consider the below shown loading conditions. Which one will fail first according to distortion energy theory? [take, σ/τ = 2]
I.
II. 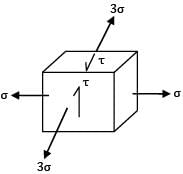
An I-beam with flanges of size 200 mm × 200 mm and a web of 600 mm × 12 mm is subjected to a bending moment of 450 kNm and a shear force of 400 kN at a section. The major principal stress at a point 200 mm above the neutral axis is __________ MPa
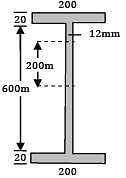
(A) 114.0
(B) 116.0
A circle of diameter 500 mm is inscribed on a square plate of copper, before the application of stresses as shown, σ1 = 160 MPa, σ2 = 80 MPa, τ = 30 MPa. After the application of stresses, the circle is deformed into an ellipse. Then the major and minor axes of the ellipse will be Given E = 100 GPa, ν = 0.35.

|
37 videos|39 docs|45 tests
|
|
37 videos|39 docs|45 tests
|



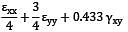
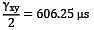
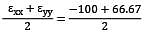 = −16.665 μs
= −16.665 μs = −83.33 μs
= −83.33 μs
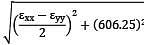
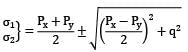
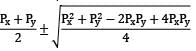
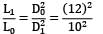
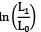
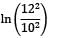

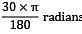

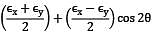

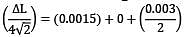

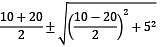

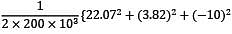 = −2(0.3)[(22.07 × 3.82) + (3.82 × −10) + (−10 × 22.07)]}
= −2(0.3)[(22.07 × 3.82) + (3.82 × −10) + (−10 × 22.07)]}

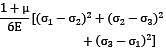
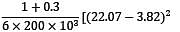 + +(3.82 + 10)2 + (−10 − 22.07)2]
+ +(3.82 + 10)2 + (−10 − 22.07)2]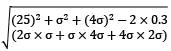


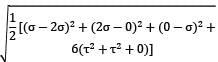

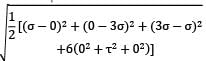
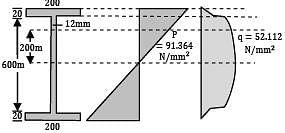
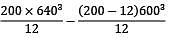



 = 52.112 N/mm2
= 52.112 N/mm2
















