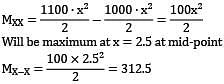Test: SFD & BMD Level - 2 - Mechanical Engineering MCQ
20 Questions MCQ Test Strength of Materials (SOM) - Test: SFD & BMD Level - 2
Match List-I with List-II and select the correct answer using codes given below the lists.

Codes:



| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If the shear force acting at every section of a beam is of the same magnitude and of the same direction then it represents a
If the bending moment at a section of a beam is zero then
The nature of combined stress in a beam depends on the nature of (where P(axial load) M(Bending moment))
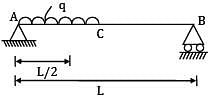
A simply supported beam of span L, carries uniformly distributed load of intensity ‘q’ over one half of the span. Shear force at mid-span section is
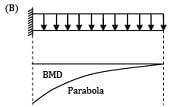
A loaded beam is shown in the figure. The bending moment diagram of the beam is best represented as
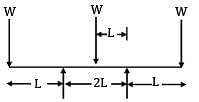
The shearing force diagram for a beam is shown in the above figure. The bending moment diagram is represented by which one of the following?

The figure shows the shear force diagram for an overhanging beam ACDB.
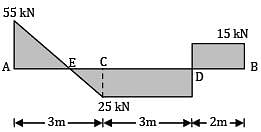
Consider the following statements with respect to the above beam
1. The beam has supports at A and D
2. The beam carries a concentrated load at C of 25 kN
3. Bending moment at D is 15 kNm
4. The beam carries a uniformly distributed load of 80 kN over the portion AC.
Which of the statements given above is/are correct?
A central concentrated load causes a maximum bending moment M in a simply supported beam. If the same load is distributed uniformly over the entire span, the maximum bending moment is
Which of the following statement are true
I. At the point of concentrated load, there is a change in shear load in SFD and slope of curve is BMD
II. At the point of concentrated moment, there is no change in shear load in SFD but there is a change in moment in BMD
Beam A B C is 8 m long and is simply supported at A and at a point B such that AB = 6m. A point load of 1.5 T acts at C and a total u. d. l of 8 T acts over half of AB. The shear force at A in Tons would be
A beam with length ‘l’ between the pinned supports overhangs by ‘a’ and both sides. Then mid-span bending moment in the beam is zero under uniformly distributed load covering the entire span, if
The loading on a simply supported beam of span 10 m is given as u. d. l, q = 20 kN/m, 4m ≤ x ≤ 10 m. The shear force at mid-span section is
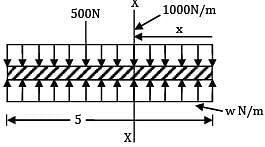
A wooden log of length 5m is floating in water. Its self-weight is 1kN/m. If a man of weight 500 N is standing at the mid span, the maximum B.M. is
The given figure shown a beam BC simply supported at C and hinged at B (free end) of a cantilever AB. The beam and the cantilever carry forces of

100kg and 200kg are respectively. The bending moment at B is
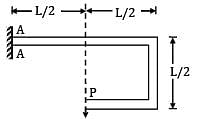
A beam subjected to a load P is shown in the given figure. The bending moment at the support AA of the beam will be
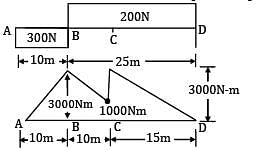
Shear force and bending moment diagrams for a beam ABCD are shown in figure. It can be concluded that
|
37 videos|39 docs|45 tests
|
|
37 videos|39 docs|45 tests
|