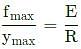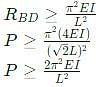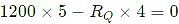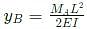Test: Simple Stress & Strain Level - 1 - Mechanical Engineering MCQ
20 Questions MCQ Test Strength of Materials (SOM) - Test: Simple Stress & Strain Level - 1
A plane-strain compression (forging) of a block is shown in the figure. The strain in the z-direction is zero. The yield strength (Sy) in uniaxial tension/compression of the material of the block is 300 MPa and it follows the Tresca (maximum shear stress) criterion. Assume that the entire block has started yielding. At a point where σx=40MPa (compressive) and τxy=0, the stress component σy is


At a critical point in a component, the state of stress is given as σxx=100MPa, σyy=220MPa, σxy=σyx=80MPa and all other stress components are zero. The yield strength of the material is 468 MPa. The factor of safety on the basis of maximum shear stress theory is ______ (round off to one decimal place).
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A prismatic, straight, elastic, cantilever beam is subjected to a linearly distributed transverse load as shown below. If the beam length is L, Young's modulus E, and area moment of inertia I, the magnitude of the maximum deflection is


Consider two concentric circular cylinders of different materials M and N in contact with each other at r=b, as shown below. The interface at r=b is frictionless. The composite cylinder system is subjected to internal pressure P. Let  denote the radial and tangential displacement and stress components, respectively, in material M. Similarly,
denote the radial and tangential displacement and stress components, respectively, in material M. Similarly,  denote the radial and tangential displacement and stress components, respectively, in material N. The boundary conditions that need to be satisfied at the frictionless interface between the two cylinders are:
denote the radial and tangential displacement and stress components, respectively, in material N. The boundary conditions that need to be satisfied at the frictionless interface between the two cylinders are:
The state of stress at a point in a component isrepresented by a Mohr's circle of radius 100MPa centered at 200 MPa on the normal stress axis. On a plane passing through the same point, the normal stress is 260 MPa. The magnitude of the shear stress on the same plane at the same point is ______ MPa.
A wire of circular cross-section ofdiameter 1.0 mm is bent into a circular arc of radius 1.0 m by application of pure bending moments at its ends. The Young's modulus of the material of the wire is 100 GPa. The maximum tensile stress developed in the wire is ______MPa.
Uniaxial compression test data for a solid metal bar of length 1 m is shown in the figure.

The bar material has a linear elastic response from O to P followed by a non-linear response. The point P represents the yield point of the material. The rod is pinned at both the ends. The minimum diameter of the bar so that it does not buckle under axial loading before reaching the yield point is _______ mm (round off to one decimal place).
Consider a linear elastic rectangular thin sheet of metal, subjected to uniform uniaxial tensile stress of 100 MPa along the length direction. Assume plane stress conditions in the plane normal to the thickness. The Young's modulus E=200 MPa and Poisson's ratio v=0.3 are given. The principal strains in the plane of the sheet are
The loading and unloading response of a metal is shown in the figure. The elastic and plastic strains corresponding to 200 MPa stress, respectively, are

The stress state at a point in a material under plane stress condition is equi-biaxial tension with a magnitude of 10 MPa. If one unit on the σ−τ plane is 1 MPa, the Mohr's circle representation of the state-of-stress is given by
Bars of square and circular cross-section with 0.5 m length are made of a material with shear strength of 20 MPa. The square bar cross-section dimension is 4 cm x 4 cm and the cylindrical bar cross-section diameter is 4 cm. The specimens are loaded as shown in the figure.

Which specimen(s) will fail due to the applied load as per maximum shear stress theory?
The barrier shown between two water tanks of unit width (1 m) into the plane of the screen is modeled as a cantilever.

Taking the density of water as 1000 kg/m3, and the acceleration due to gravity as m/s2, the maximum absolute bending moment developed in the cantilever is ______ kNm (round off to the nearest integer).
The truss shown in the figure has four members of length l and flexural rigidity EI, and one member of length l√2 and flexural rigidity 4EI. The truss is loaded by a pair of forces of magnitude P, as shown in the figure.

The smallest value of P, at which any of the truss members will buckle is
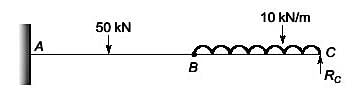
The magnitude of reaction force at joint C of the hinge-beam shown in the figure is _______ kN (round off to 2 decimal places).

A beam of negligible mass is hinged at support P and has a roller support Q as shown in the figure.

A point load of 1200 N is applied at point R. The magnitude of the reaction force at support Q is __________ N.
A cantilever of length l, and flexural rigidity EI, stiffened by a spring of stiffness k, is loaded by transverse force P, as shown
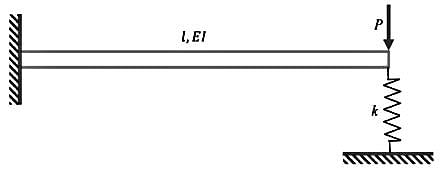
The transverse deflection under the load is
A thin-walled cylinder of radius r and thickness t is open at both ends, and fits snugly between two rigid walls under ambient conditions, as shown in the figure.

The material of the cylinder has Young's modulus E, Poisson's ratio v, and coefficient of thermal expansion
α. What is the minimum rise in temperature ΔT of the cylinder (assume uniform cylinder temperature with no buckling of the cylinder) required to prevent gas leakage if the cylinder has to store the gas at an internal pressure of p above the atmosphere?
A cantilever beam of length, L, and flexural rigidity, EI, is subjected to an end moment, M, as shown in the figure. The deflection of the beam at x=L/2 is

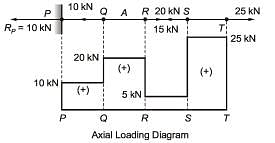
A prismatic bar PQRST is subjected to axial loads as shown in the figure. The segments having maximum and minimum axial stresses, respectively, are

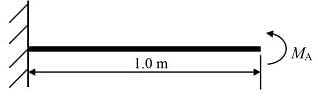
A horizontal cantilever beam of circular cross-section, length 1.0 m and flexural rigidity EI= 200 N⋅m2 is subjected to an applied moment MA= 1.0 N⋅m at the free end as shown in the figure. The magnitude of the vertical deflection of the free end is _______mm (round off to one decimal place).
|
37 videos|39 docs|45 tests
|
|
37 videos|39 docs|45 tests
|


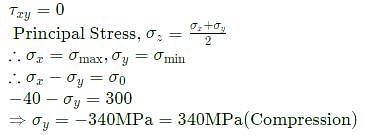
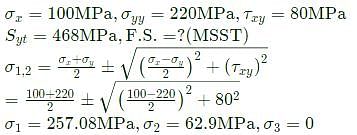
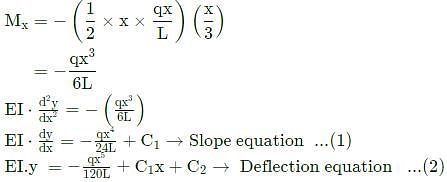

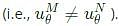 Similarly the Hoop stress at point of contact need not be same
Similarly the Hoop stress at point of contact need not be same 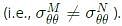 As the interface will be always in contact the displacement in radial direction and stress in radial directions must be same for two cylinders. i.e.,
As the interface will be always in contact the displacement in radial direction and stress in radial directions must be same for two cylinders. i.e.,