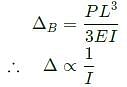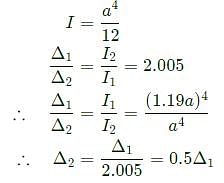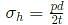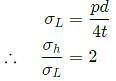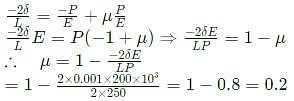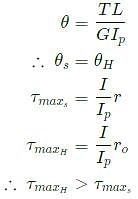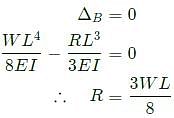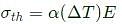Test: Simple Stress & Strain Level - 2 - Mechanical Engineering MCQ
20 Questions MCQ Test Strength of Materials (SOM) - Test: Simple Stress & Strain Level - 2
The cross sections of two hollow bars made of the same material are concentric circles as shown in the figure. It is given that r3>r1 and r4>r2 and that the areas of the cross-sections are the same.J1 and J2 are the torsional rigidities of the bars on the left and right, respectively. The ratio J2/J1 is


A cantilever beam having square cross-section of side a is subjected to an end load. If a is increased by 19%, the tip deflection decreases approximately by
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
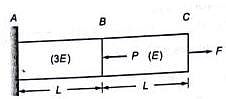
A horizontal bar with a constant cross-section is subjected to loading as shown in the figure. The Young's moduli for the sections AB and BC are 3E and E, respectively

For the deflection at C to be zero, the ratio P/F is ____________

For the deflection at C to be zero, the ratio P/F is ____________
A hypothetical engineering stress-strain curve shown in the figure has three straight lines PQ, QR, RS with coordinates P(0,0), Q(0.2,100), R(0.6,140) and S(0.8,130). 'Q' is the yield point, 'R' is the UTS point and 'S' the fracture point.
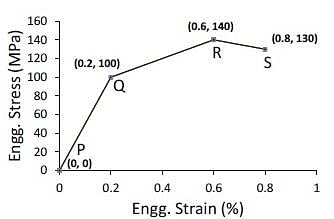
The toughness of the material (in MJ/m3) is __________
A machine element XY, fixed at end X, is subjected to an axial load P, transverse load F, and a twisting moment T at its free end Y. The most critical point from the strength point of view is

A thin cylindrical pressure vessel with closed-ends is subjected to internal pressure. The ratio of circumferential (hoop) stress to the longitudinal stress is
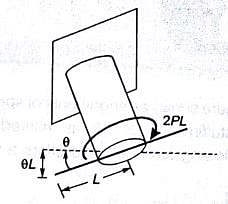
A rigid horizontal rod of length 2L is fixed to a circular cylinder of radius R as shown in the figure. Vertical forces of magnitude P are applied at the two ends as shown in the figure. The shear modulus for the cylinder is G and the Young's modulus is E.

The vertical deflection at point A is
A square plate of dimension L x L is subjected to a uniform pressure load p = 250 MPa on its edges as shown in the figure. Assume plane stress conditions. The Young's modulus E = 200 GPa.
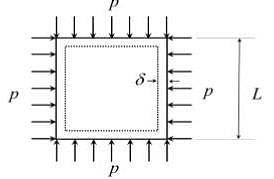
The deformed shape is a square of dimension L−2δ . If L= 2 m and δ=0.001 m, the Poisson's ratio of the plate material is __________
Two circular shafts made of same material, one solid (S) and one hollow (H), have the same length and polar moment of inertia. Both are subjected to same torque. Here, θs is the twist and τs is the maximum shear stress in the solid shaft, whereas θH is the twist and τH is the maximum shear stress in the hollow shaft. Which one of the following is TRUE?
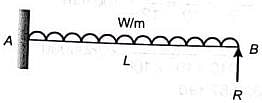
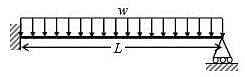
A beam of length L is carrying a uniformly distributed load w per unit length. The flexural rigidity of the beam is EI. The reaction at the simple support at the right end is
The poisson's ratio for a perfectly incompressible linear material is
A motor is driving a solid circular steel shaft transmits 40kW of power at 500 rpm. If the diameter of the shaft is 40 mm, The maximum shear stress in the shaft is ____MPa.
Consider a beam with circular cross-section of diameter d. The ratio of the second moment of area about the neutral axis to the section modulus of the area is.
In the engineering stress-strain curve for mild steel, the Ultimate Tensile Strength (UTS) refers to
A cantilever beam of length L and flexural modulus EI is subjected to a point load P at the free end. The elastic strain energy stored in the beam due to bending (neglecting transverse shear) is
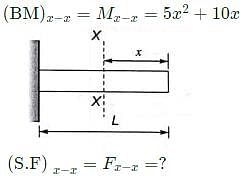
For a loaded cantilever beam of uniform cross-section, the bending moment (in N.mm) along the length is M(x)=5x2+10x , where x is the distance (in mm) measured from the free end of the beam. The magnitude of shear force (in N) in the cross-section at x=10 mm is
A steel bar is held by two fixed supports as shown in the figure and is subjected to an increases of temperature ΔT=100∘C.If the coefficent of thermal exapnasion and young's modules of elasticity of steel are 11×10−6/∘C and 200GPa, respectively, the magnitude of thermal stress (in MPa) induced in the bar is _____

A rod of length 20mm is stretched to make a rod of length 40 mm. Subsequently, it is compressed to make a rod of final length 10 mm. Consider the longitudinal tensile strain as positive and compressive strain as negative. The total true longitudinal strain in the rod is_______
If σ1 and σ3 are the algebraically largest and smallest principal stresses respectively, the value of the maximum shear stress is
For an Oldham coupling used between two shafts, which among the following statements are correct?
I. Torsional load is transferred along shaft axis.
II. A velocity ratio of 1:2 between shafts is obtained without using gears.
III. Bending load is transferred transverse to shaft axis.
IV. Rotation is transferred along shaft axis.
|
37 videos|39 docs|45 tests
|
|
37 videos|39 docs|45 tests
|