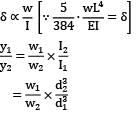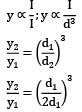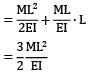Test: Slope & Deflection Level - 1 - Mechanical Engineering MCQ
15 Questions MCQ Test Strength of Materials (SOM) - Test: Slope & Deflection Level - 1
Other parameters being unchanged, if the span of a cantilever carrying end point load is doubled, the maximum slope is increased by
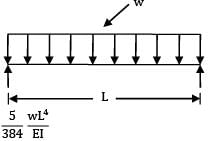
A cantilever beam of span L is carrying a uniformly distributed load of intensity w/unit length on the entire span. The deflection at the free end is given by
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
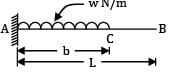
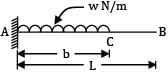
A cantilever of length ‘L’ is carrying a uniformly distributed load ‘w’ per unit run for a distance of ‘b’ from fixed end. The slope at the free end is given as
A cantilever beam of span L, uniform flexural rigidity EI is subjected to a unit couple at its free end. The deflection at the Centre of the beam is
A cantilever of length of span ‘L’ carries a uniformly distributed load of w per unit length over its entire span. If its span is halved, then its slope will become
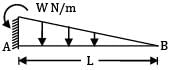
A cantilever beam of span ‘L’ is carrying a triangular load of zero intensity at its free end to W per unit length at its fixed end. the deflection at its free end will be
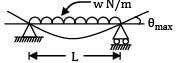
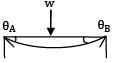
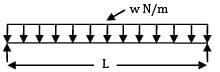
Slope at the end of the simply supported beam of span ‘L’ with uniformly distributed load w/unit length over the entire span is given by
A beam of length ‘L’ simply supported at the ends carries a point load W at distance 'a' from the left end. Also L − a = b. The deflection under load is given by
A simply supported beam of span L carries a UDL of w. N m−1. What is the magnitude of concentrated load to be supplied at the centre of this beam which would produce the same deflection as the UDL?
A simply supported beam of span L carries a concentrated load w at mid-span. The slope at the end is given by (EI = constant for total length)
A simply supported beam of span ‘L’ carries a uniformly distributed load, 'w' per unit length over the entire span. The deflection at the center is 'y'. If the distributed load per unit length is doubled and also the depth of beam is doubled, the deflection at the center would be
If the actual beam has both ends fixed, then the ends of the conjugate beam will be
A cantilever beam AB is fixed at left end A and free at B. The corresponding conjugate beam will supports
A beam simply supported at the ends carries a load W at the Centre, causing deflection y. If the depth of the section of the beam is doubled, the deflection at the Centre will be
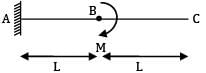
For cantilever beam shown in figure, the deflection at C due to a couple M applied at B is equal to
|
37 videos|39 docs|45 tests
|
|
37 videos|39 docs|45 tests
|