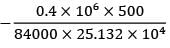Test: Torsion Level - 3 - Mechanical Engineering MCQ
10 Questions MCQ Test Strength of Materials (SOM) - Test: Torsion Level - 3
Two shafts are made of the same material and same outer diameter. With one having a circular section, and the other a hollow circular section with inner diameter, half that of outer diameter. The torque that can be transmitted by the solid section is N times that of the hollow section, where N is
A solid phosphor bronze shaft 60 mm in diameter is rotating at 800 rpm and transmitting power. It is subjected to torsion only. An electrical resistance strain gauge mounted on the surface of the shaft, gives the strain reading as 3.98 × 10−4 . If the modulus of elasticity for bronze is 105 GN/m2 and Poisson’s ratio 0.3. The power transmitted by the shaft will be (Bending effect may be neglected) (Gage is mounted at 45o to the shaft axis).
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
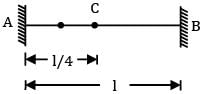
A round shaft of diameter 'd' and length 'l' fixed at both ends 'A' and 'B' is subjected to a twisting moment ‘T’ at 'C', at a distance of l/4 from A (see figure). The torsional stresses in the parts AC and CB will be

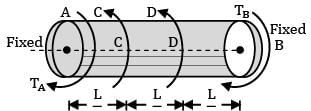
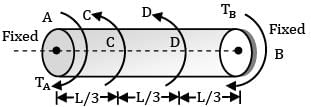
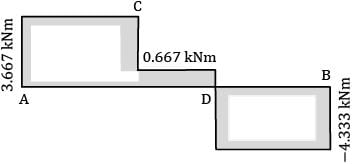
A horizontal shaft, L m long, is rigidly fixed at both the ends. At section C and D, torques 3 kNm (ccw) and 5 kNm (ccw) looking from the side A are applied. What are the fixing couples TA and TB?
In a torsion test, the specimen is a hollow shaft with 50 mm external diameter and 30 mm internal diameter. An applied torque of 1.6 kNm is found to produce an angular twist of 0.40° measured on a length of 0.2 m of the shaft. Young’s modulus of elasticity obtained from the elastic test has been found to be 200 GPa.
Then the Poisson’s ratio will be
Two beams are of same length and same weight. One beam is of solid circular section and the other is a hollow section. The internal diameter is half of the external diameter. The ratio of the strength of hollow section to that of solid section is
A circular section rod ABC is fixed at ends A and C. It is subjected to torque T at B. !B = BC = L and the polar moment of inertia of portions AB and BC are 2 J and J respectively. If G is the modulus of rigidity, what is the angle of twist at point B?
A solid circular rod AB of diameter D and length L is fixed at both ends. A torque T is applied at a section x such that !X = L/4 and BX = 3L/4. What is the maximum shear stress developed in the rod?
A hollow shaft having an inside diameter 60% of its outside diameter is to replace a solid shaft transmitting the same power at the same speed. If the material is the same, the percentage saving in the materials is
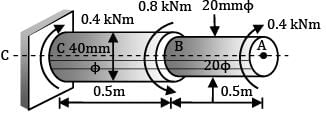
A stepped shaft ABC, 1m long made of steel is of diameter 20 mm from A to B = 0.5m, 40 mm from B to C = 0.5 m. It is subjected to a twisting moment of 0.4 kNm (cw) at A, 0.8 kNm (ccw) at B and 0.4 kNm (cw) at C. If G = 84 N/mm2, the angular twist between A and C. (in degrees) is ______________
|
37 videos|39 docs|45 tests
|
|
37 videos|39 docs|45 tests
|


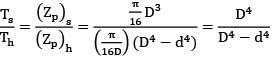
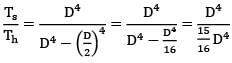

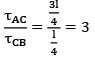
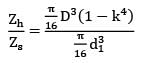
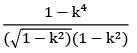
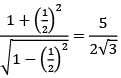
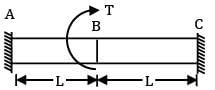

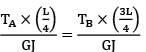
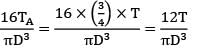
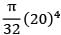 = 1.5708 × 104 mm4
= 1.5708 × 104 mm4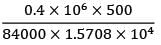
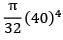 = 25.132 × 104 mm4
= 25.132 × 104 mm4