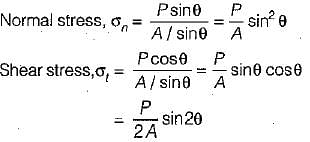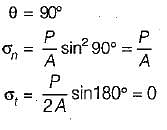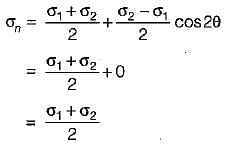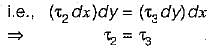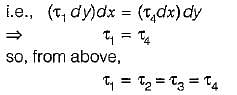Test: Analysis of Stress & Strain - 1 - Mechanical Engineering MCQ
10 Questions MCQ Test Strength of Materials (SOM) - Test: Analysis of Stress & Strain - 1
A bar of square cross - section has b ee n subjected to an axial tensile load. A plane normal to the axis of loading will have
Normal stresses of equal magnitude a but of opposite signs act at a point of a strained material in perpendicular direction. What would be the resultant normal stress on a plane inclined at 45° to the applied stresses?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
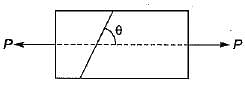
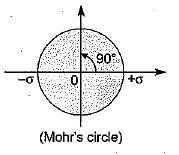
With reference to the following figure, the tangential stress σt on a plane inclined at an angle θ to the line of action of σ1 would be
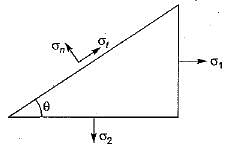

For an element under the effect of biaxial state of normal stresses, the normal stress on 45° plane is equal to
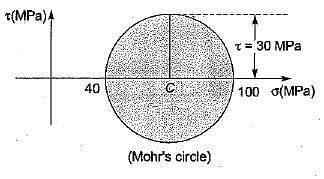
If the principal stresses on a plane stress problem are σ1 = 100 MPa and σ2 = 40 MPa, then the magnitude of shear stress (in MPa) will be
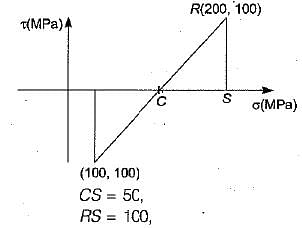
The state of plane stress at a point is given by σx = 200 MPa, σy = 100 MPa and τxy = 100 MPa. The maximum shear stress (in MPa) is then
The state of stresses on an element is as shown in following figure.
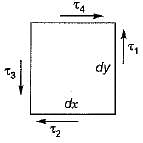
The necessary and sufficient condition for its equilibrium is
|
37 videos|39 docs|45 tests
|
|
37 videos|39 docs|45 tests
|