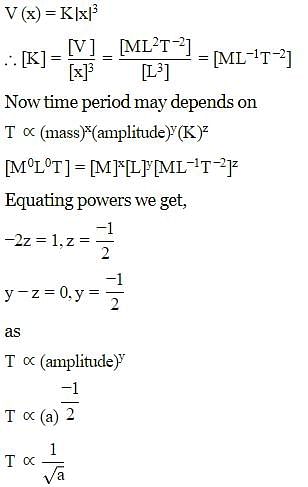Test: Dynamics of Simple Harmonic Motion - NEET MCQ
10 Questions MCQ Test Topic-wise MCQ Tests for NEET - Test: Dynamics of Simple Harmonic Motion
A particle of mass m is executing oscillation about the origin on X-axis. Its potential energy is V(x)=K∣x∣3. Where K is a positive constant. If the amplitude of oscillation is a, then its time period T is proportional to.
The dimensions and unit of phase constant Φ is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If the reference particle P moves in uniform circular motion, its projection along a diameter of the circle executes
The equation of motion of a particle is x= 3cos(0.45t+π/4)m. Its maximum acceleration is
If the sign in equation F = -kx is changed what would happen to the motion of the oscillating body?
Choose the correct time period of the function sin ωt + cos ωt
The velocity and acceleration amplitudes of body executing simple harmonic motion is
At what distance from the mean position would the K.E of a particle in simple harmonic motion be equal to its potential energy?
What is the maximum Kinetic energy and minimum potential energy of a harmonic oscillator with amplitude 0.03m, force constant 4×105 N/m and total mechanical energy of 230 J.
A particle starts S.H.M. from the mean position. Its amplitude is A and time period is T. At the time when its speed is half of the maximum speed, its displacement y is
|
9 docs|1272 tests
|