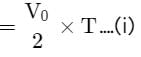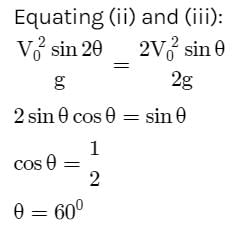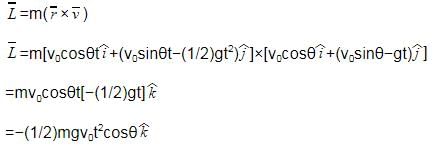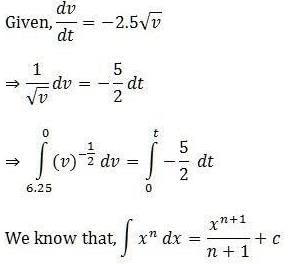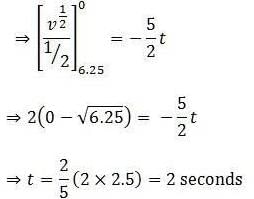Test: JEE Previous Year Questions- Motion in a Straight Line - JEE MCQ
28 Questions MCQ Test Physics for JEE Main & Advanced - Test: JEE Previous Year Questions- Motion in a Straight Line
If a body losses half of its velocity on penetrating 3 cm in a wooden block, then how much will it penetrate more before coming to rest?
[AIEEE 2002]
From a building, two balls A and B are thrown such that A is thrown upwards and B downwards (both vertically with the same velocity). If vA and vB are their respective velocities on reaching the ground, then:
[AIEEE 2002]
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A ball whose kinetic energy is E is projected at an angle of 45° to the horizontal. The kinetic energy of the ball at the highest point of its flight will be:
[AIEEE 2002]
Speeds of two identical cars u and 4u at a specific instant. The ratio of the respective distances at which the two cars are stopped from that instant by the same braking force:
[AIEEE 2002]
The coordinates of a moving particle at any time t are given by 
and 
. The speed of the particle at time t is given by:
[AIEEE 2003]
A boy playing on the roof of a 10 m high building throws a ball with a speed of 10 m/s at an angle of 30° with the horizontal. How far from the throwing point will the ball be at the height of 10 m from the ground? [g = 10 m/s2, sin 30° = 1/2, cos 30° = √3/2]
[AIEEE 2003]
A car moving with a speed of 50 km/h, can be stopped by brakes after at least 6 m. If the same car is moving at a speed of 100 km/h, the minimum stopping distance is:
[AIEEE 2003]
A ball is thrown from a point with a speed v0 at an angle of projection θ. From the same point and at the same instant, a person starts running with a constant speed v0 / 2 to catch the ball. Will the person be able to catch the ball? If yes, what should be the angle of projection?
[AIEEE 2004]
A particle is acted upon by a force of constant magnitude which is always perpendicular to the velocity of the particle. The motion of the particle takes place in a plane, it follows that:
[AIEEE 2004]
An automobile travelling at a speed of 60 km/h, can apply the brake to stop within a distance of 20 m. If the car is going twice as fast, i.e. 120 km/h, the stopping distance will be:
[AIEEE 2004]
A ball is released from the top of a tower of height h meter. It takes T seconds to reach the ground. What is the position of the ball in T/3 seconds?
[AIEEE 2004]
A parachutist after bailing outfalls 50 m without friction. When the parachute opens, it decelerates at 2 ms-2. He reaches the ground with a speed of 3 ms-1. At what height, did he bail out?
[AIEEE 2005]
A particle is moving eastwards with a velocity of 5 ms-1. In 10 s the velocity changes to 5 ms-1 northwards. The average acceleration in this time is:
[AIEEE 2005]
A car, starting from rest, accelerates at the rate f through a distance s, then continues at a constant speed for time t and then decelerates at the rate f/2 to come to rest. If the total distance travelled is 15 s, then:
[AIEEE 2005]
The relation between time t and distance x is t = ax2 + bx, where a and b are constants. The acceleration is:
[AIEEE 2005]
A projectile can have the same range R for two angles of projection. If t1 and t2 be the times of flights in the two cases, then the product of the two times of flights is proportional to:
[AIEEE 2005]
A particle located at x = 0 at time t = 0, starts moving along the positive x-direction with a velocity v that varies as 
. The displacement of the particle varies with time as:
[AIEEE 2006]
A particle is projected at 60° to the horizontal with a kinetic energy K. The kinetic energy at the highest point is:
[AIEEE 2007]
The velocity of a particle is 
. If its position is x = 0 at t = 0, then its displacement after unit time (t = 1) is:
[AIEEE 2007]
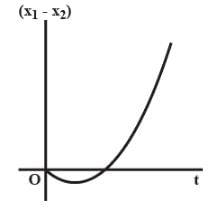
A body is at rest at x = 0. At t = 0, it starts moving in the positive x-direction with a constant acceleration. At the same instant, another body passes through x = 0 moving in the positive x-direction with a constant speed. The position of the first body is given by x1 (t) after time t and that of the second body by x2(t) after the same time interval. Which of the following graphs correctly describes (x1 – x2) as a function of time?
[AIEEE 2008]
Consider a rubber ball freely falling from a height h = 4.9 m onto a horizontal elastic plate. Assume that the duration of the collision is negligible and the collision with the plate is totally elastic. Then the velocity as a function of time the height as a function of time will be:
[AIEEE 2009]
A particle has initial velocity (2i + 3j) and acceleration (0.3i + 0.2j). The magnitude of velocity after 10 s will be:
A small particle of mass m is projected at an angle θ with the x-axis with an initial velocity v0 in the x-y plane as shown in the figure. At a time 
, the angular momentum of the particle is:
[AIEEE 2010]
A particle is moving with velocity 
where k is a constant. The general equation for its path is:
[AIEEE 2010]
A water fountain on the ground sprinkles water all around it. If the speed of water coming out of the fountain is v, the total area around the fountain that gets wet is:
[AIEEE 2011]
An object, moving with a speed of 6.25 m/s, is decelerated at a rate given by 
where v is the instantaneous speed. The time taken by the object, to come to rest, would be:
[AIEEE 2011]
A boy can throw a stone up to a maximum height of 10 m. The maximum horizontal distance that the boy can throw the same stone up to will be:
[AIEEE 2012]
A particle of mass m is at rest at the origin at time t = 0. It is subjected to a force F(t) = F0e-bt in the x-direction. Its speed v(t) is depicted by which of the following curves?
[AIEEE 2012]
|
289 videos|635 docs|179 tests
|
|
289 videos|635 docs|179 tests
|
Top Courses for JEE
Important Questions for JEE Previous Year Questions- Motion in a Straight Line
JEE Previous Year Questions- Motion in a Straight Line MCQs with Answers
Online Tests for JEE Previous Year Questions- Motion in a Straight Line Physics for JEE Main & Advanced
|
© EduRev
|
Education Revolution
|
|
