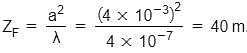Test: Wave Optics - NEET MCQ
30 Questions MCQ Test Physics Class 12 - Test: Wave Optics
Referring to the Young’s double slit experiment, Phase difference corresponding to a Path Difference of λ /3 is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The angle of incidence at which the reflected beam is fully polarized is called
The refractive index of glass is 1.5 which of the two colors red and violet travels slower in a glass prism?
In a young’s double slit experiment, the central bright fringe can be identified by
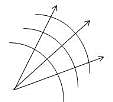
Shape of the wave front of light diverging from a point source is
In a Young’s double-slit experiment, the slits are separated by 0.28 mm and the screen is placed 1.4 m away. The distance between the central bright fringe and the fourth bright fringe is measured to be 1.2 cm. Determine the wavelength of light used in the experiment
Shape of the wave front of light emerging out of a convex lens when a point source is placed at its focus.
A beam of light consisting of two wavelengths, 650 nm and 520 nm, is used to obtain interference fringes in a Young’s double-slit experiment. Find the distance of the third bright fringe on the screen from the central maximum for wavelength 650 nm.
A beam of light has a wavelength of 650 nm in vacuum. What is the wavelength of these waves in the liquid whose index of refraction at this wavelength is 1.47?
A beam of light consisting of two wavelengths, 650 nm and 520 nm, is used to obtain interference fringes in a Young’s double-slit experiment. What is the least distance from the central maximum where the bright fringes due to both the wavelengths coincide?
A parallel beam of light in air makes an angle of 47.5∘ with the surface of a glass plate having a refractive index of 1.66. What is the angle between the reflected part of the beam and the surface of the glass?
Shape of the wave front of portion of the wave front of light from a distant star intercepted by the Earth
Which of the following phenomenon cannot be explained by diffraction?
Estimate the distance for which ray optics is good approximation for an aperture of 4 mm and wavelength 400 nm.
The critical angle for total internal reflection at a liquid–air interface is 42.5∘ If a ray of light traveling in air has an angle of incidence at the interface of 35∘ what angle does the refracted ray in the liquid make with the normal?
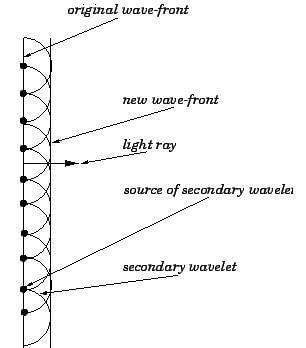
According to Huygens construction relation between old and new wave fronts is
We say that a light wave is linearly polarized in y direction if
A parallel beam of light of wavelength 500 nm falls on a narrow slit and the resulting diffraction pattern is observed on a screen 1 m away. It is observed that the first minimum is at a distance of 2.5 mm from the centre of the screen. Find the width of the slit.
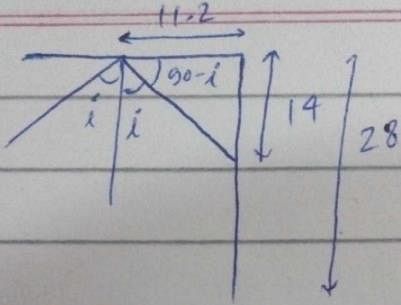
Two plane mirrors intersect at right angles. A laser beam strikes the first of them at a point 11.5 cm from their point of intersection, as shown in figure For what angle of incidence at the first mirror will this ray strike the midpoint of the second mirror (which is 28.0 cm long) after reflecting from the first mirror?

If we have two coherent sources S1andS2 vibrating in phase, then for an arbitrary point P constructive interference is observed whenever the path difference is
|
98 videos|387 docs|104 tests
|