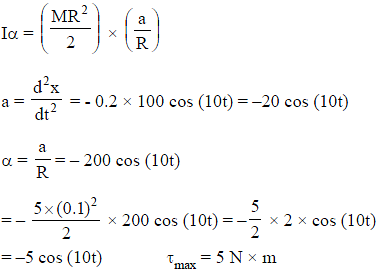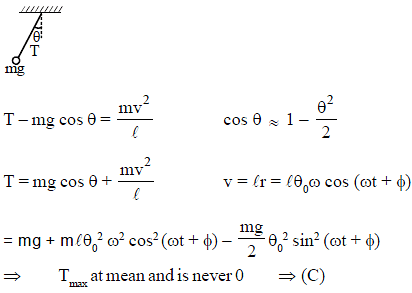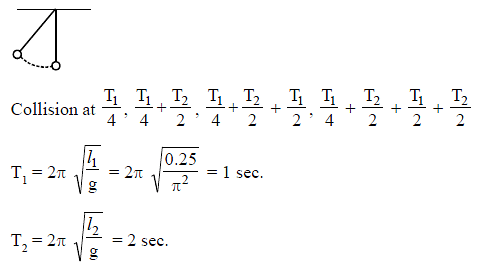Chapter Test: SHM - JEE MCQ
30 Questions MCQ Test Physics for JEE Main & Advanced - Chapter Test: SHM
A solid disk of radius R is suspended from a spring of linear spring constant k and torsional constant c, as shown in figure. In terms of k and c, what value of R will give the same period for the vertical and torsional oscillations of this system?

The periodic time of S.H.M. of amplitude 2 cm is 5 sec. If the amplitude is made 4 cm, its periodic time will be -
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The motion of a particle is expressed by the equation acc. a = – bx where x is displacement from equilibrium position and b is constant. What is the periodic time ?
A simple pendulum 4 m long swings with an amplitude of 0.2 m. What is its acceleration at the ends of its path ?
(g = 10 m/s2)
The equation of SHM of a particle is a + 4π2x = 0 where α is instantaneous linear acceleration at displacement x, the frequency of motion is -
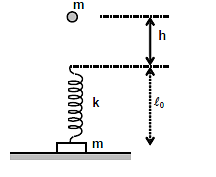
In the figure shown a massless spring of stiffness 100 N/m and natural length l0 m is rigidly attached to a block of mass 20 kg and is in vertical position. A wooden ball of mass m is released from rest to fall under gravity. Having fallen through a height h the ball strikes the spring and gets stuck up in the spring at the top. What should be the minimum value of h (in cm) so that the lower block will just lose contact with the ground later on? Neglect any loss of energy.
A body is executing SHM. When the displacement from the mean position is 4cm and 5 cm. The values of the corresponding velocity of the body are 10 cm s–1 and 8 cm s–1. Then the time period of the body is -
A particle at the end of a spring executes simple harmonic motion with a period t1, while the corresponding period for another spring is t2. If the period of oscillation with the two springs in series is T, then -
A particle performs harmonic oscillations along a straight line with a period T and amplitude a. The mean velocity of the particle averaged over the time interval during which it travels a distance a/2 starting from the extreme position is :
Particle moves on the x-axis according to the equation x = A + B sin ωt. The motion is simple harmonic with amplitude.
A system is shown in the figure. The time period for small oscillations of the two blocks will be -
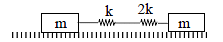
The acceleration-displacement (a-x) graph of a particle executing simple motion is shown in figure. The frequency of oscillation is given by -
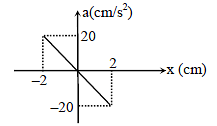
A particle is vibrating in simple harmonic motion with an amplitude of 4 cm. At what displacement from the equilibrium position is its energy half potential and half kinetic ?
A pendulum of length 200 cm is horizontal when its bob of mass 200 gm is released. It has 90% of initial energy when the bob reaches the lower most point. Speed of the bob at this point is -
A simple pendulum with angular frequency ω oscillates simple harmonically. The tension in the string at lowest point is T. The total acceleration of the bob at its lowest position is -
A second pendulum is mounted in a space shuttle. Its period of oscillations will decrease when rocket is:
A particle of mass 10 gm lies in a potential field v = (50x2+100) J/kg. The value of frequency of oscillations in Hz is
In simple harmonic motion the displacement of a particle from its equilibrium position is given by 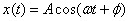 . Here the phase of motion is
. Here the phase of motion is
Find the amplitude of the S.H.M whose displacement y in cm is given by equation y= 3 sin157t + 4 cos157t, where t is time in seconds.
A particle executes linear simple harmonic motion with an amplitude of 2 cm. When the particle is at 1 cm from the mean position, the magnitude of its velocity is equal to that of its acceleration. Then its time period in seconds is:
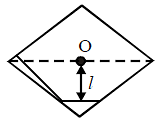
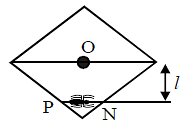
A square metal frame in the vertical plane is hinged at O at its center. A bug moves along the rod PN which is at a distance l from the hinge, such that the whole frame is always stationary, even though the frame is free to rotate in the vertical plane about the hinge. Then the motion of the bug will be simple harmonic, with time period
A uniform solid cylinder of mass 5 kg and radius 0.1 m is resting on a horizontal platform (parallel to the x-y plane) and is free to rotate about its axis along the y-axis. The platform is given a motion in the x direction given by x = 0.2 cos(10t) m. If there is no slipping, then maximum torque acting on the cylinder during its motion is
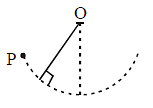
A short boy sits on a seat suspended by a light string from a fixed point O and starts swinging in a vertical plane from the extreme position P with a small amplitude. The graph, which shows the variation of the tension in the string with time ‘t’ is :
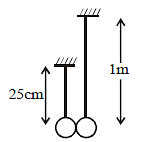
Two small bobs of same mass are hung from two threads of different length as shown. The bobs are just touching each other. Now the left bob is pulled out by a small angle (θ < 10°)="" in="" same="" vertical="" plane="" and="" released="" at="" t="0." it="" collides="" with="" the="" other="" bob.="" at="" what="" time(s)="" the="" two="" bobs="" do="" not="" collide="" with="" each="" />
A body is executing SHM. When the displacement from the mean position is 4cm and 5 cm. The values of the corresponding velocity of the body are 10 cm s–1 and 8 cm s–1. Then the time period of the body is -
|
289 videos|635 docs|179 tests
|
|
289 videos|635 docs|179 tests
|


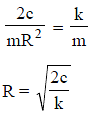
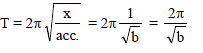

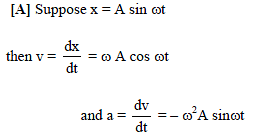
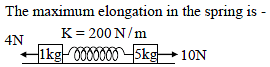
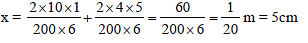
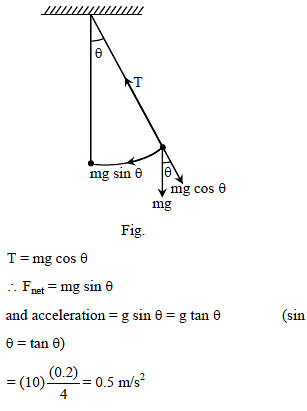
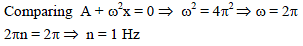


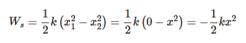
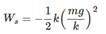
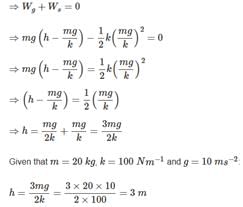
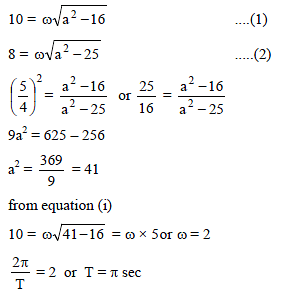
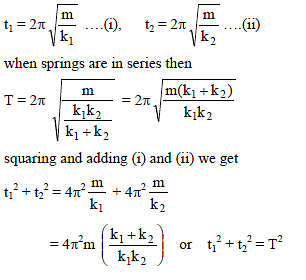



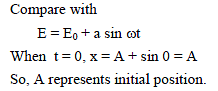
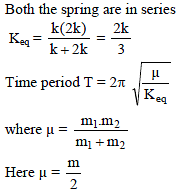
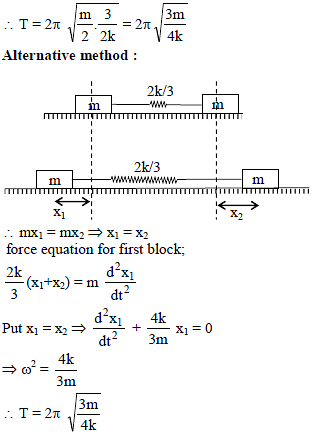
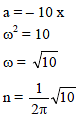
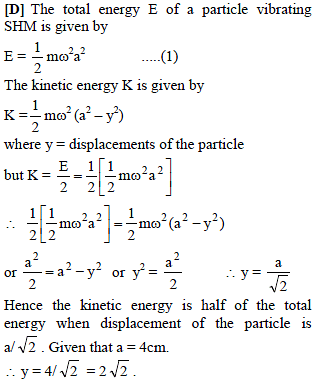
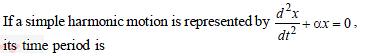
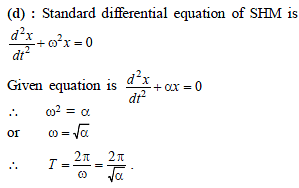

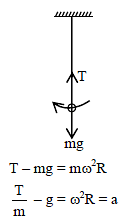
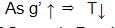
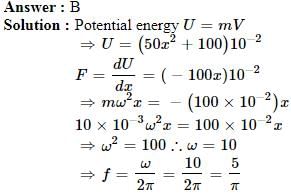
 ∴ We get, ω = √3 s-1
∴ We get, ω = √3 s-1