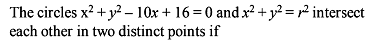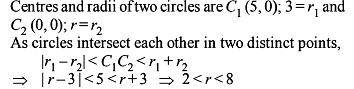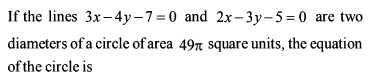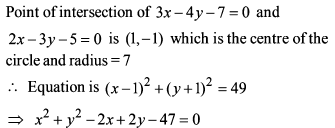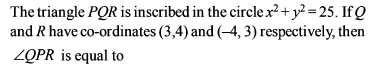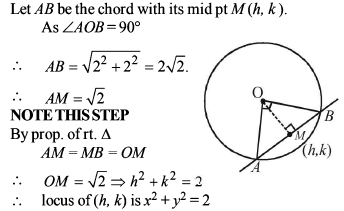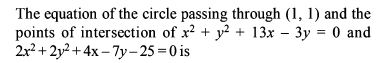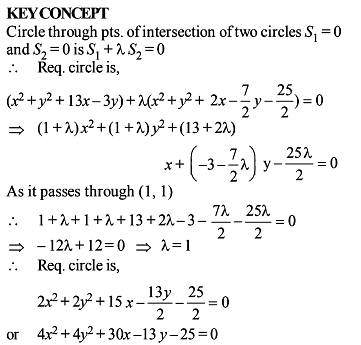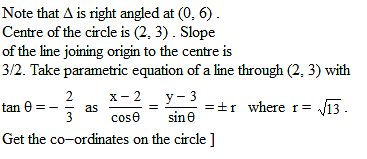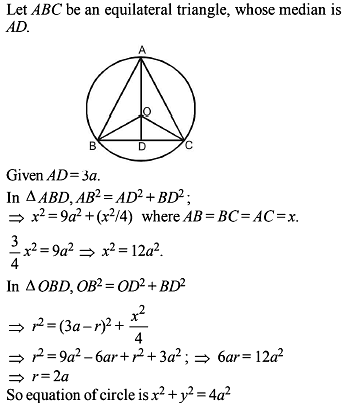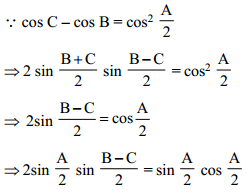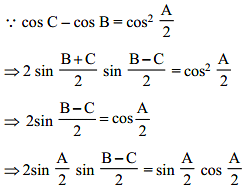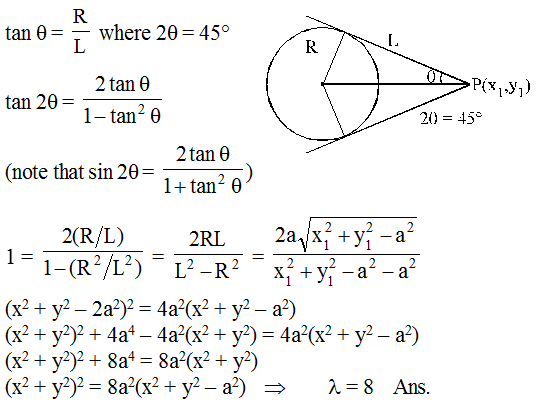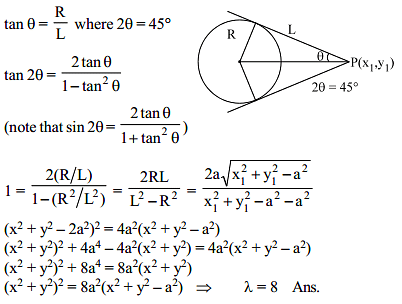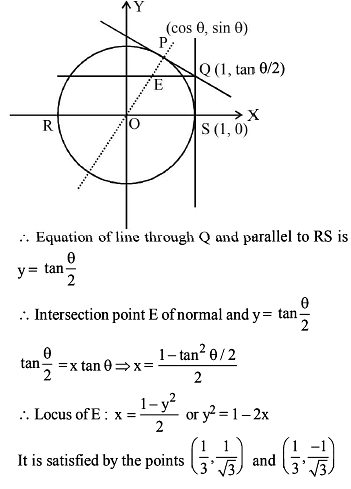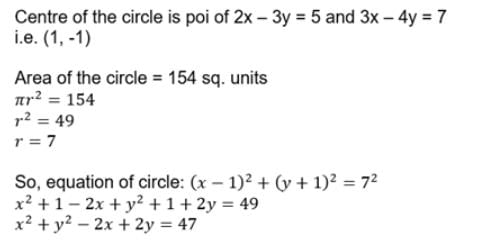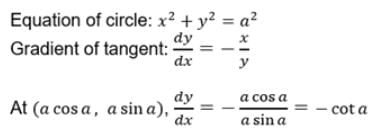Circle - 1 - JEE MCQ

The possible radius of a circle whose centre is at the origin and which touches the circle x² + y² – 6x – 8y + 21 = 0, is

A circle passes through the points (- 1, 1) ,  (0, 6) and  (5, 5) . The point(s) on this circle, the tangent(s) at which is/are parallel to the straight line joining the origin to its centre is/are :

In a triangle ABC with fixed base BC, the vertex A moves such that cos C – cos B = cos² A/2 . If a, b and c denote the lengths of sides of the triangle opposite to angles A, B and C, respectively, then which one of the following is correct?

The locus of the point of intersection of the tangent to the circle x² + y² = a², which include an angle of 45° is the curve  (x² + y²)² = λa2 (x² + y² – a²). The value of λ is

The locus of the point of intersection of the tangent to the circle x² + y² = a², which include an angle of 45° is the curve 

(x² + y²)² = λa² (x² + y² – a²). The value of λ is

The possible radius of a circle whose centre is at the origin and which touches the circle x² + y² – 6x – 8y + 21 = 0, is

The lines 2x – 3y = 5 and 3x – 4y = 7 are diameters of a circle of area 154 sq. units. The equation of the circle is

The equation of the circle passing through (3, 6) and whose centre is (2, –1) is

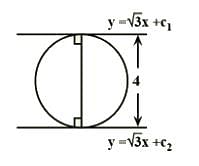
y = √3x + c₁ & y = √3x + c₂ are two parallel tangents of a circle of radius 2 units, then |c₁ – c₂| is equal to

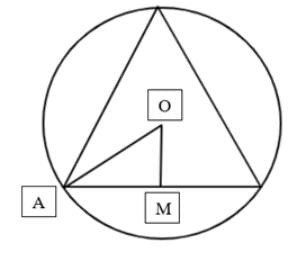
The area of an equilateral triangle inscribed in the circle x² + y² – 2x = 0 is

The gradient of the tangent line at the point (a cos a, a sin a) to the circle x² + y² = a², is

The greatest distance of the point P(10, 7) from the circle x² + y² – 4x – 2y – 20 = 0 is