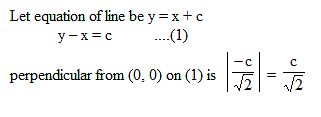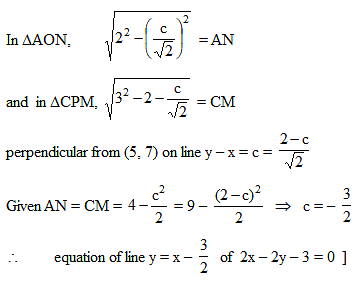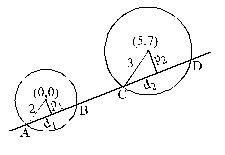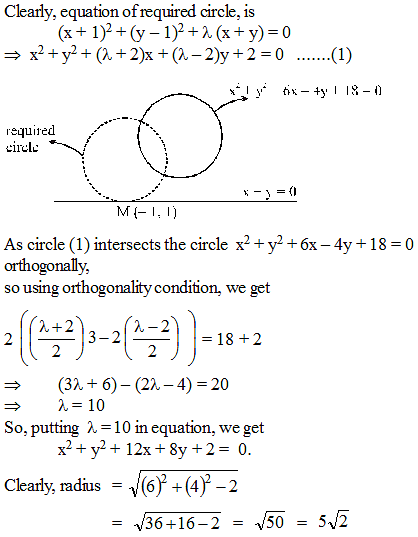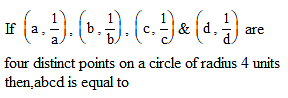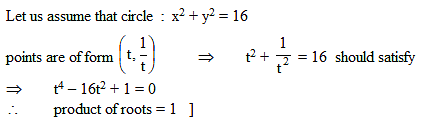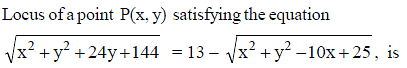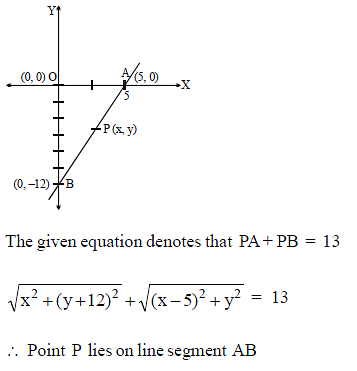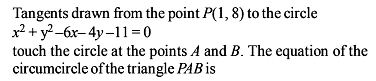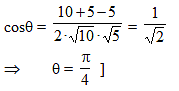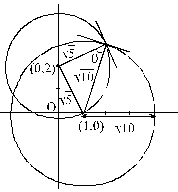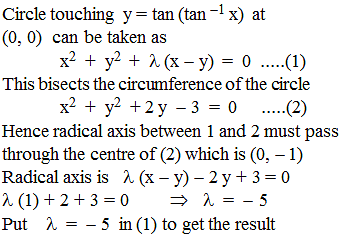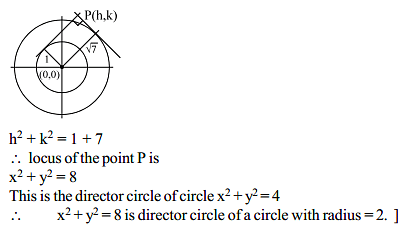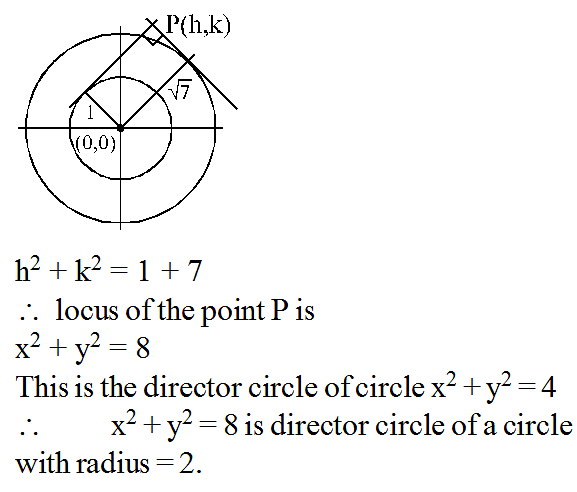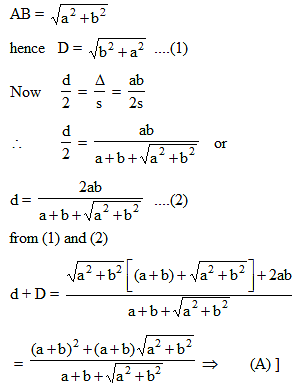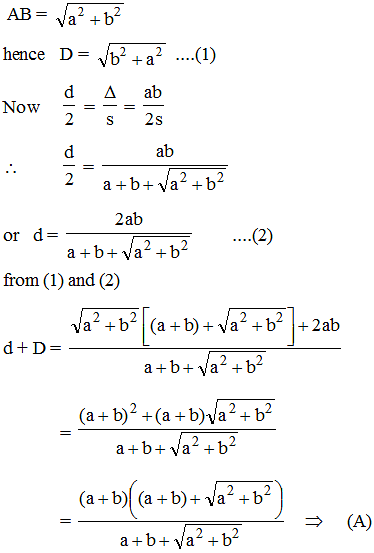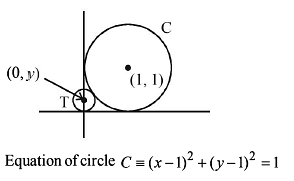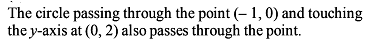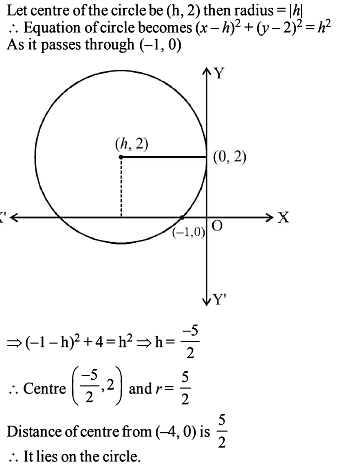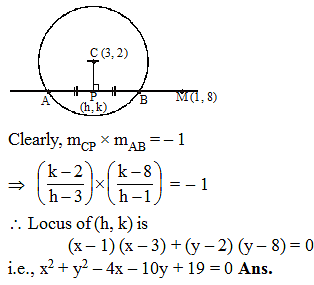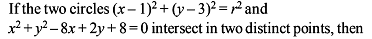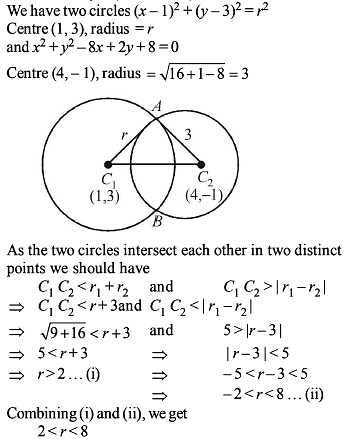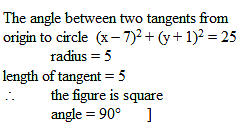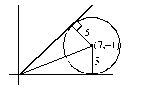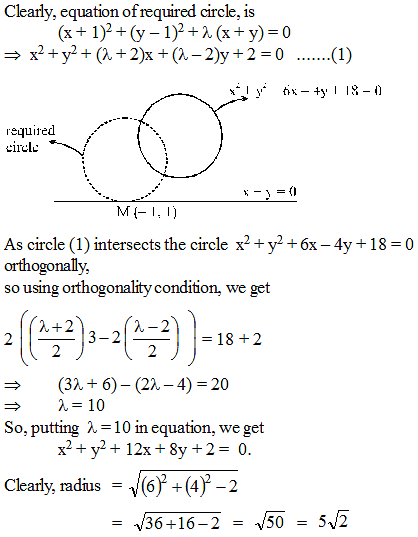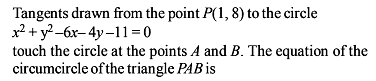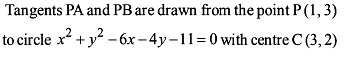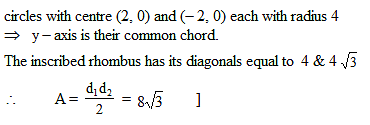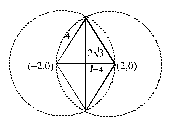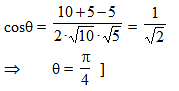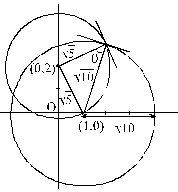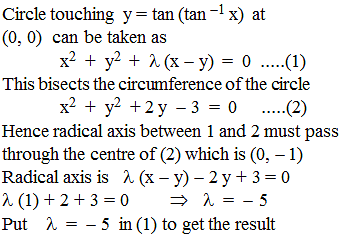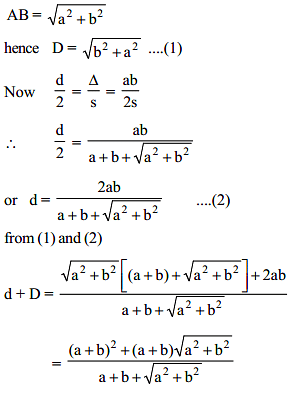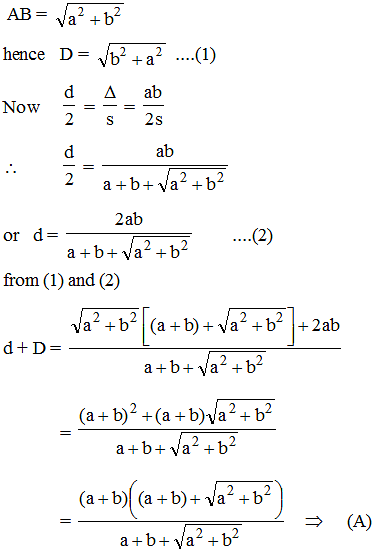Circle - 2 - JEE MCQ
30 Questions MCQ Test Mathematics (Maths) for JEE Main & Advanced - Circle - 2
The radius of the circle which touches the line x + y = 0 at M (– 1, 1) and cuts the circle x2 + y2 + 6x – 4y + 18 = 0 orthogonally, is
The angle at which the circles (x – 1)2 + y2 = 10 and x2 + (y – 2)2 = 5 intersect is
Equation of the circle which bisects the circumference of the circle x2 + y2 + 2 y - 3 = 0 and touches the curve y = tan (tan–1 x) at the origin is :
Locus of the point of intersection of the pair of perpendicular tangents to the circles x2 + y2 = 1 and x2 + y2 = 7 is the director circle of the circle with radius.
Locus of the point of intersection of the pair of perpendicular tangents to the circles x2 + y2 = 1 and x2 + y2 = 7 is the director circle of the circle with radius.
Let a and b represent the length of a right triangle's legs. If d is the diameter of a circle inscribed into the triangle, and D is the diameter of a circle superscribed on the triangle, then d + D equals
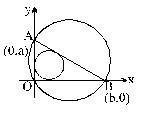
Let a and b represent the length of a right triangle's legs. If d is the diameter of a circle inscribed into the triangle, and D is the diameter of a circle superscribed on the triangle, then d + D equals

The possible radius of a circle whose centre is at the origin and which touches the circle x2 + y2 – 6x – 8y + 21 = 0, is
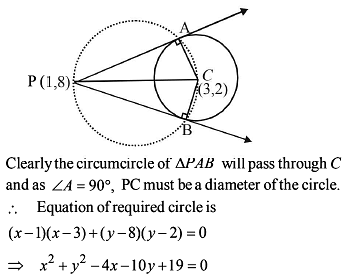
The locus of the midpoints of the chords drawn from the point M (1, 8) to the circle x2 + y2 – 6x – 4y – 11 = 0, is equal to
The angle between the two tangents from the origin to the circle (x - 7)2 + (y + 1)2 = 25 equals
The radius of the circle which touches the line x + y = 0 at M (– 1, 1) and cuts the circle x2 + y2 + 6x – 4y + 18 = 0 orthogonally, is
A rhombus is inscribed in the region common to the two circles x2 + y2 - 4x - 12 = 0 and x2 + y2 + 4x - 12 = 0 with two of its vertices on the line joining the centres of the circles. The area of the rhombous is :
The angle at which the circles (x – 1)2 + y2 = 10 and x2 + (y – 2)2 = 5 intersect is
Equation of the circle which bisects the circumference of the circle x2 + y2 + 2 y - 3 = 0 and touches the curve y = tan (tan–1 x) at the origin is :
Let a and b represent the length of a right triangle's legs. If d is the diameter of a circle inscribed into the triangle, and D is the diameter of a circle superscribed on the triangle, then d + D equals
Locus of the point of intersection of the pair of perpendicular tangents to the circles x2 + y2 = 1 and x2 + y2 = 7 is the director circle of the circle with radius.
Let a and b represent the length of a right triangle's legs. If d is the diameter of a circle inscribed into the triangle, and D is the diameter of a circle superscribed on the triangle, then d + D equals
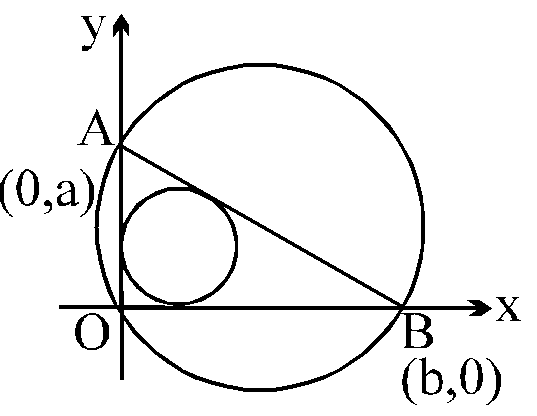
|
209 videos|443 docs|143 tests
|
|
209 videos|443 docs|143 tests
|