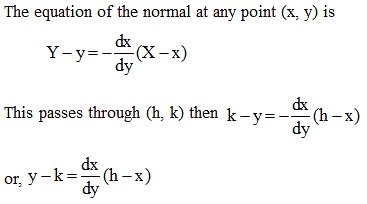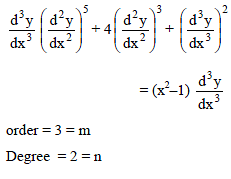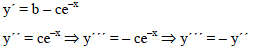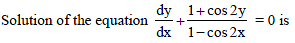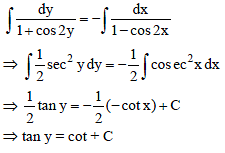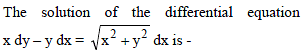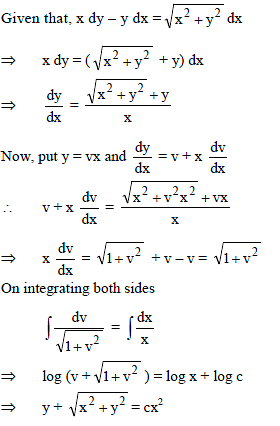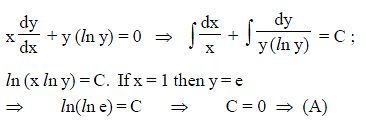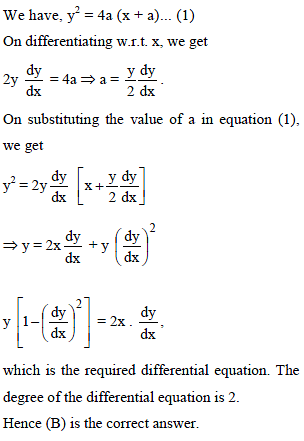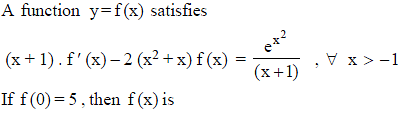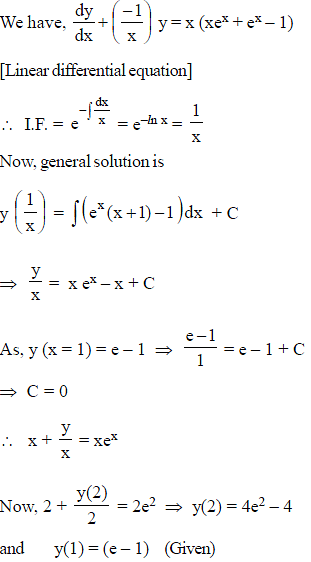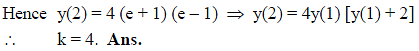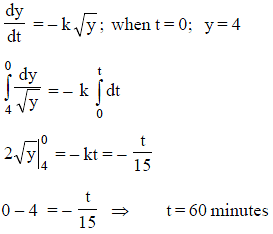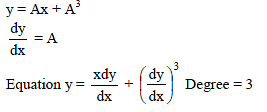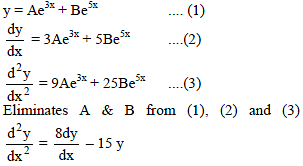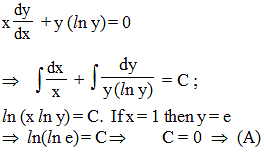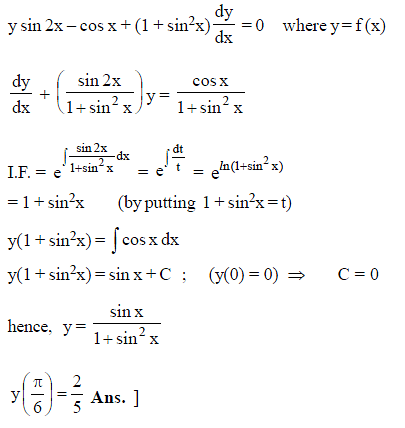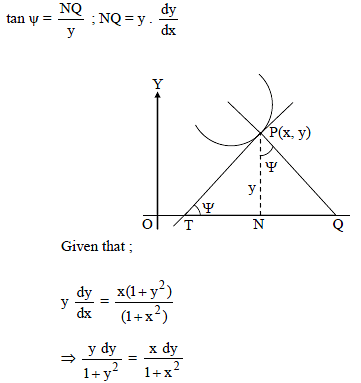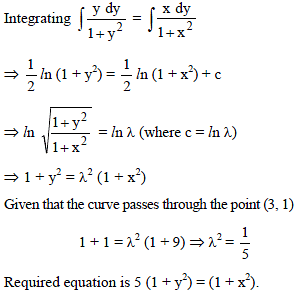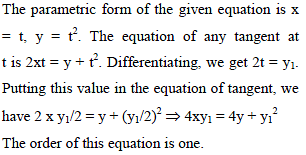Differential Equations - 1 - JEE MCQ
30 Questions MCQ Test Mathematics (Maths) for JEE Main & Advanced - Differential Equations - 1
The differential equation of the curve for which the normal at every point passes through a fixed point (h, k) is
The differential equation of the family of curves represented by y = a + bx + ce–x (where a, b, c are abritrary constants) is -
Solution of differential equation (2x cos y + y2 . cos x)dx + (2y . sin x – x2 . sin y)dy = 0 is –
The solution of the differential equation y lny + xy' = 0, where y (1) = e, is
The degree of the differential equation, of which y2 = 4a (x + a) is a solution, is -
Water is drained from a vertical cylindrical tank by opening a valve at the base of the tank. It is known that the rate at which the water level drops is proportional to the square root of water depth y, where the constant of proportionality k > 0 depends on the acceleration due to gravity and the geometry of the hole. If t is measured in minutes and k = 1/15 then the time to drain the tank if the water is 4 meter deep to start with is
Family y = Ax + A3 of curve represented by the differential equation of degree -
The differential equation of the family of curves y = Ae3x + Be5x, where A and B are arbitrary constants, is -
The solution of the differential equation y lny + xy' = 0, where y (1) = e, is
A function y = f (x) satisfies the differential equation f(x) · sin 2x – cos x + (1 + sin2x) f ' (x) = 0 with initial condition y (0) = 0. The value of f (π/6) is equal to
The order of the differential equation of all tangent lines to the parabola y = x2 is
|
209 videos|443 docs|143 tests
|
|
209 videos|443 docs|143 tests
|