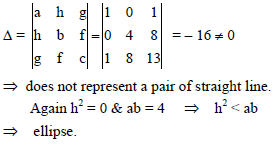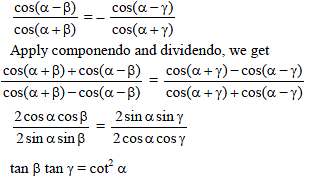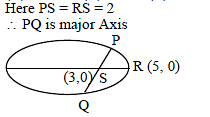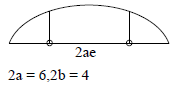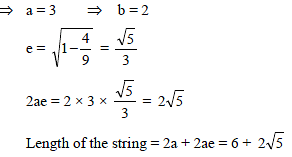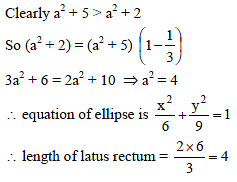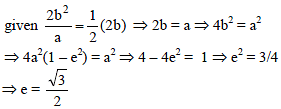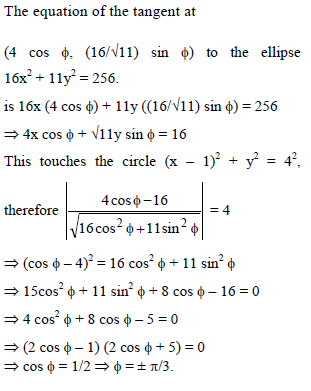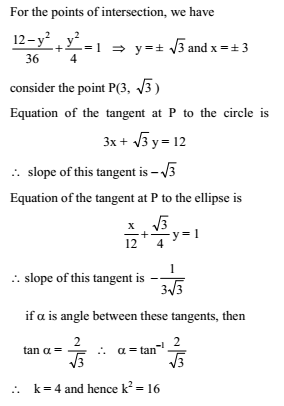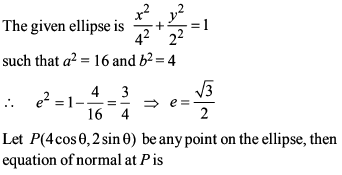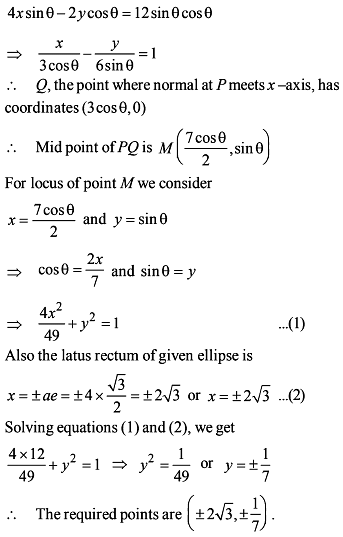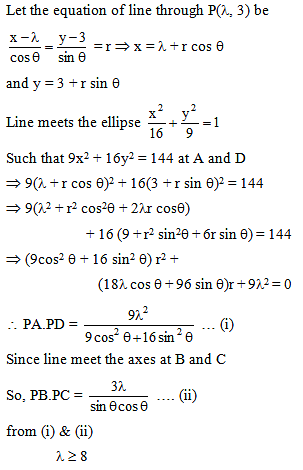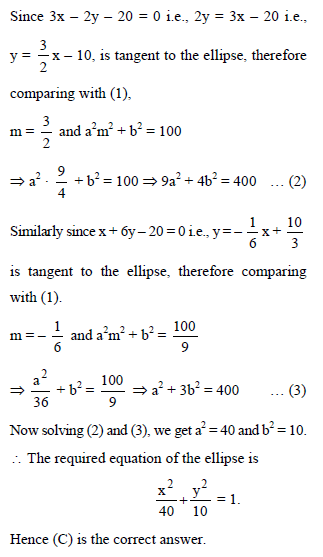Ellipse - 1 - JEE MCQ
30 Questions MCQ Test Mathematics (Maths) for JEE Main & Advanced - Ellipse - 1
The second degree equation x2 + 4y2 + 2x + 16y +13 = 0 represent itself as -
PQ and QR are two focal chords of an ellipse and the eccentric angles of P,Q,R and 2α, 2β, 2γ respectively then tan β tan γ is equal to -
An ellipse is described by using an endless string which is passed over two pins. If the axes are 6 cm and 4 cm, the necessary length of the string and the distance between the pins respectively in cm are-
If the latus rectum of an ellipse be equal to half of its minor axis, then its eccentricity is
If the tangent at the point (4 cos ϕ , (16/√11) sin ϕ) to the ellipse 16x2 + 11y2 = 256 is also a tangent to the circle x2 + y2 – 2x = 15, then the value of ϕ is -
If α, β are the eccentric angles of the extremities of a focal chord of the ellipse x2/16 + y2/9 = 1, then tan (α/2) tan (β/2) =
If C is the centre of the ellipse 9x2 + 16y2 = 144 and S is one focus. The ratio of CS to semimajor axis, is -
The equation of the ellipse whose axes are coincident with the co-ordinate axes and which touches the straight lines 3x – 2y – 20 = 0 and x + 6y – 20 = 0, is -
|
209 videos|443 docs|143 tests
|
|
209 videos|443 docs|143 tests
|