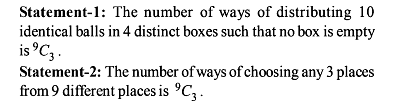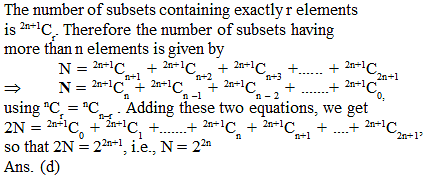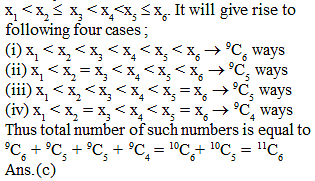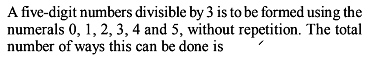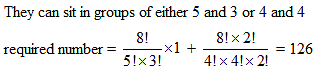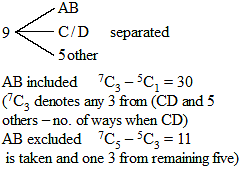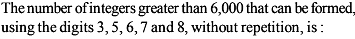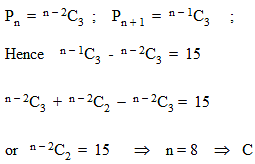Permutations and Combinations - 1 - JEE MCQ
30 Questions MCQ Test Mathematics (Maths) for JEE Main & Advanced - Permutations and Combinations - 1
The number of different ways in which a man can invite one or more of his 6 friends to dinner is
The number of all three digit even numbers such that if 5 is one of the digits then next digit is 7 is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A coin is tossed n times, the number of all the possible outcomes is
The number of ways in which the 4 faces of a regular tetrahedron can be painted with 4 different colours is
In a multiple choice question, there are 4 alternatives, of which one or more are correct. The number of ways in which a candidate can attempt this question is
The number of arrangements of n different things taken r at a time which exclude a particular thing is
All possible three digits even numbers which can be formed with the condition that if 5 is one of the digit, then 7 is the next digit is :
The number of ways in which we can distribute mn students equally among m sections is given by-
Find the number of five digit numbers that can be formed using the digits 1, 2, 3, 4, 5, 6, 7, 8, 9 in which one digit appears once and two digits appear twice (e.g. 41174 is one such number but 75355 is not.).
A set contains 2n + 1 elements. The number of subsets of this set which contains more than n elements is -
Total number of ways in which 15 identical blankets can be distributed among 4 persons so that each of them gets atleast two blankets, equal to
There are counters available in x different colours. The counters are all alike except for the colour. The total number of arrangements consisting of y counters, assuming sufficient number of counters of each colour, if no arrangement consists of all counters of the same colour is :
The total number of six digit numbers x1 x2 x3 x4 x5 x6 having the property that x1 < x2 ≤ x3 < x4 < x5 ≤ x6 is equal to -
A team of 8 students goes on an excursion, in two cars, of which one can seat 5 and the other only 4. If internal arrangement inside the car does not matter then the number of ways in which they can travel, is
A committee of 5 is to be chosen from a group of 9 people. Number of ways in which it can be formed if two particular persons either serve together or not at all and two other particular persons refuse to serve with each other, is
Let Pn denotes the number of ways in which three people can be selected out of ' n ' people sitting in a row , if no two of them are consecutive. If Pn + 1 - Pn = 15 then the value of 'n' is
4 letter lock consists of three rings each marked with 10 different letters, the number of ways in which it is possible to make an unsuccessful attempt to open the lock, is
|
209 videos|443 docs|143 tests
|
|
209 videos|443 docs|143 tests
|