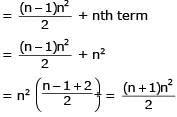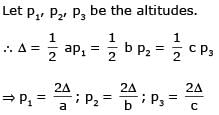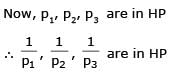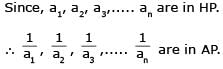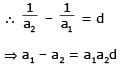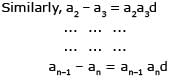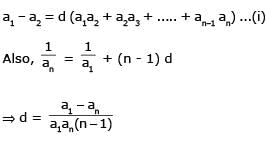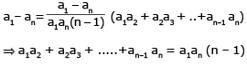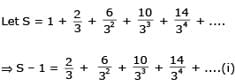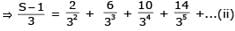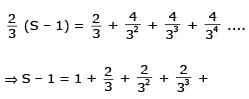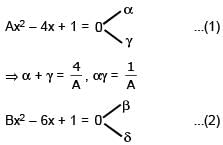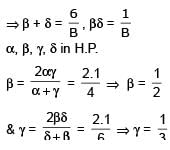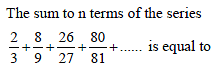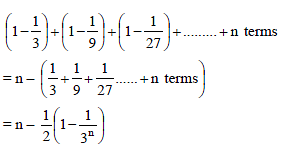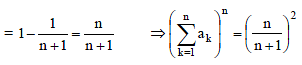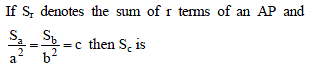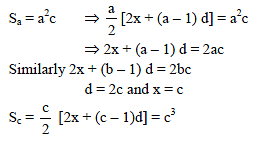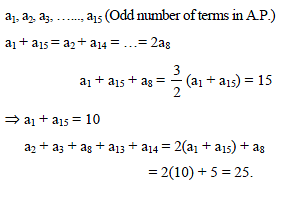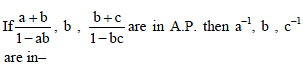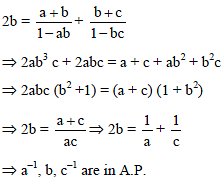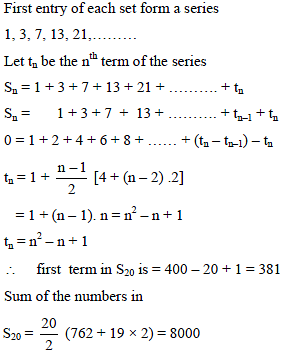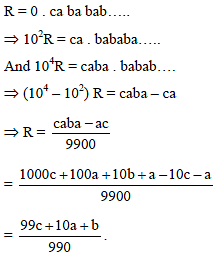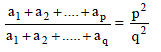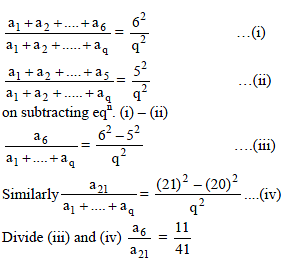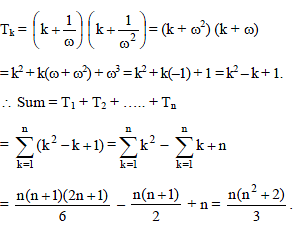Sequences and Series - 1 - JEE MCQ
30 Questions MCQ Test Mathematics (Maths) for JEE Main & Advanced - Sequences and Series - 1
If x1, x2, x3 and y1, y2, y3 are both in G.P. with the same common ratio, then the points (x1, y1), (x2, y2) and (x3, y3)
[AIEEE- 2003]
The sum of the first n terms of the series 12 + 2. 22 + 32 + 2.42 + 52 + 2.62 +..... is 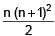 when n is even. When n is odd the sum is-
when n is even. When n is odd the sum is-
[AIEEE- 2004]
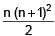 when n is even. When n is odd the sum is-
when n is even. When n is odd the sum is-| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
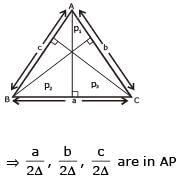
If in a ΔABC, the altitudes from the vertices A, B, C on opposite sides are in H.P., then sin A, sin B, sin C are in
[AIEEE- 2005]
If a1, a2, ..... an are in H.P., then the expression a1a2 + a2a3 +....+ an –1an is equal to –
[AIEEE- 2006]
Statement 1 : The sum of the series 1 + (1 + 2 + 4) + (4 + 6 + 9) + (9 + 12 + 16) + ...... ....+(361 + 380 + 400) is 8000.
Statement 2 : 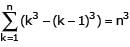 for any natural number n.
for any natural number n.
[AIEEE- 2012]
Given that α,γ are roots of the equation, Ax2–4x+1 = 0 and β, δ the roots of the equation, Bx2 – 6x + 1 = 0, find values of A and B, such that 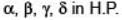
[REE 2000, 5]
In A.P. 3 + 7 + 11 + 15 + …. upto 30 terms, 12th term from end is-
If the first second and last term of an A.P. are a, b, c then the number of terms will be-
If a1, a2, a3, …..., a15 are in A.P. and a1 + a8 + a15 = 15, then a2 + a3 + a8 + a13 + a14 is equal to -
If S1 = {1}, S2 = {3, 5}, S3 = {7, 9, 11}, S4 = {13, 15, 17, 19} and so on, then the sum of all the numbers in S20 is
If a, b, c are digits then the rational number represented by 0. cababab…..is -
If (1 + 3 + 5 + … + p) + (1 + 3 + 5 + … + q) = (1 + 3 + 5 + … + r) where each set of parentheses contains the sum of consecutive odd integers as shown, the smallest possible value of p + q + r, (where p > 6) is -
The sum of all numbers of form n3 which lie between 100 and 10,000 is
|
209 videos|443 docs|143 tests
|
|
209 videos|443 docs|143 tests
|



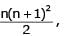 if n is even.
if n is even.