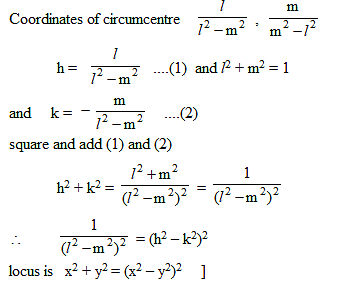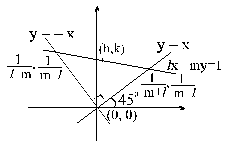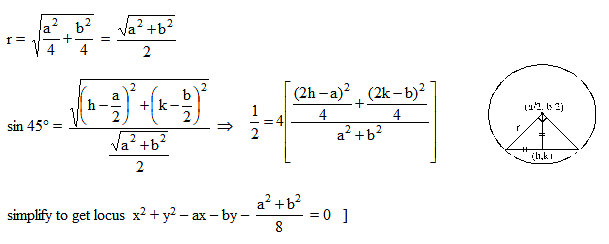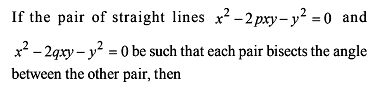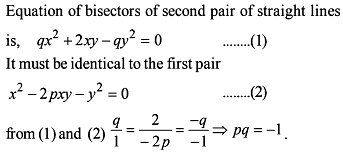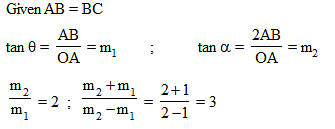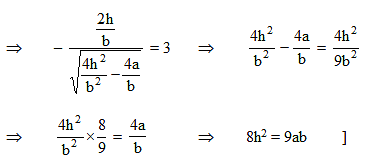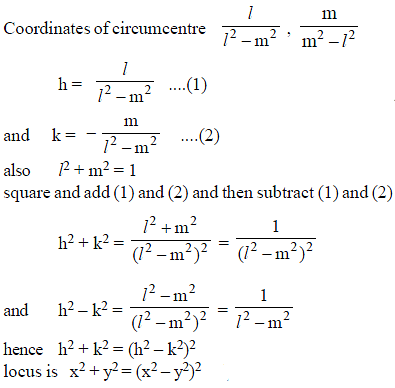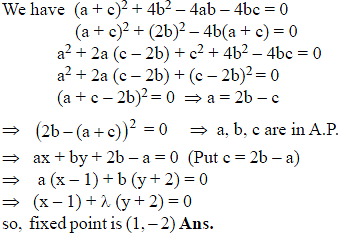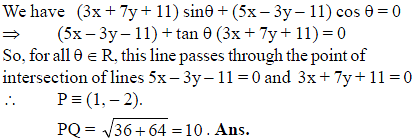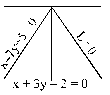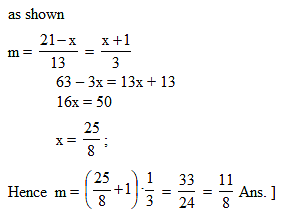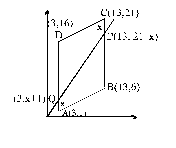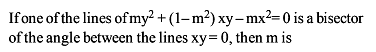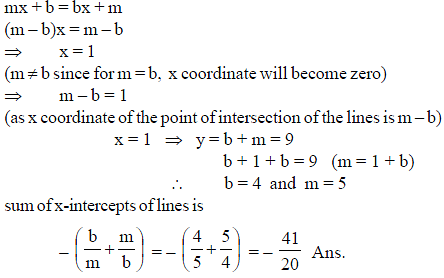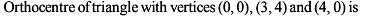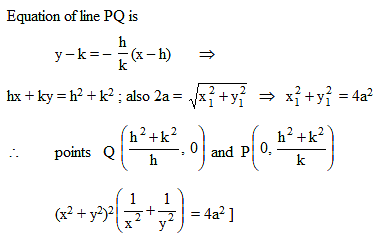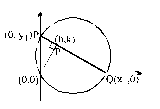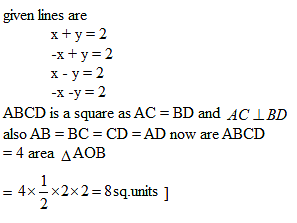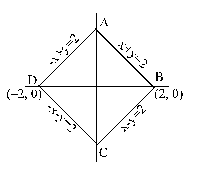Straight Lines - 2 - JEE MCQ
30 Questions MCQ Test Mathematics (Maths) for JEE Main & Advanced - Straight Lines - 2
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Triangle formed by the lines x + y = 0 , x – y = 0 and lx + my = 1. If l and m vary subject to the condition l2 + m2 = 1 then the locus of its circumcentre is
Through a point A on the x-axis a straight line is drawn parallel to y-axis so as to meet the pair of straight lines ax2 + 2hxy + by2 = 0 in B and C. If AB = BC then
Triangle formed by the lines x + y = 0 , x – y = 0 and lx + my = 1. If l and m vary subject to the condition l2 + m2 = 1, then the locus of its circumcentre is
Let a, b, c ∈ R and satisfying (a + c)2 + 4b2 – 4ab – 4bc = 0 then the variable line ax + by + c = 0 passes through a fixed point whose co-ordinates are
If all lines given by the equation (3 sin θ + 5 cos θ)x + (7 sin θ – 3 cos θ) y + 11(sin θ – cos θ) = 0 pass through a fixed point P for all θ ∈ R, then find the distance of P from Q(7, – 10).
If a, b, c form an A.P. with common difference d (≠ 0) and x, y, z form a G.P. with common ratio r ( ≠1), then the area of the triangle with vertices (a, x), (b, y) and (c, z) is indepedent of
The line x + 3y - 2 = 0 bisects the angle between a pair of straight lines of which one has equation x - 7y + 5 = 0 . The equation of the other line is :
Vertices of a parallelogram ABCD are A(3, 1), B(13, 6), C(13, 21) and D(3, 16). If a line passing through the origin divides the parallelogram into two congruent parts then the slope of the line is
The lines y = mx + b and y = bx + m intersect at the point (m – b, 9), where m ≠ b. The sum of the x-intercepts of the lines is
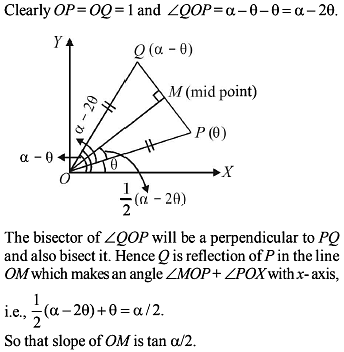
Points A & B are in the first quadrant ; point 'O' is the origin . If the slope of OA is 1, slope of OB is 7 and OA = OB, then the slope of AB is :
A circle of constant radius ' a ' passes through origin ' O ' and cuts the axes of co-ordinates in points P and Q, then the equation of the locus of the foot of perpendicular from O to PQ is :
|
209 videos|443 docs|143 tests
|
|
209 videos|443 docs|143 tests
|