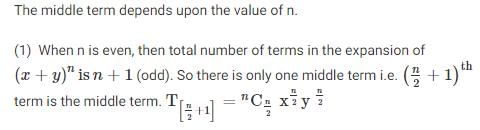Test: Binomial Theorem For Positive Index
15 Questions MCQ Test Mathematics (Maths) Class 11 | Test: Binomial Theorem For Positive Index
| 1 Crore+ students have signed up on EduRev. Have you? |
The number of terms in the expansion of (2x - 3y)8 is
Since this binomial is to the power 8, there will be nine terms in the expansion.
n = 10
Middle term = (n/2) + 1
= (10/2) + 1
= 6th term
T(6) = T(5+1)
= 10C5[(2x2)/3]5 [(3/2x2)]5
= 10C5
= 252
In the expansion of (a+b)n, N the number of terms is:
The total number of terms in the binomial expansion of (a + b)n is n + 1, i.e. one more than the exponent n.
Find the value of r, if the coefficients of (2r + 4)th and (r – 2)th terms in the expansion of (1 + x)18 are equal.
is
If the coefficients of 7th and 13th terms in the expansion of (1 + x)n are equal, then n is equal to
is
What is the coefficient of x5 in the expansion of (1-x)-6 ?
(1-x)-6
=> (1-x)(-6/1)
It is in the form of (1-x)(-p/q), p =6, q=1
(1-x)(-p/q) = 1+p/1!(x/q)1 + p(p+q)/2!(x/q)2 + p(p+q)(p+2q)/3!(x/q)3 + p(p+q)(p+2q)(p+3q)/4!(x/q)4........
= 1+6/1!(x/1)1 + 6(7)/2!(x/1)2 + 6(7)(8)/3!(x/1)3 + 6(7)(8)(9)/4!(x/1)4 +.......................
So, coefficient of x5 is (6*7*8*9*10)/120
= 252
In the expansion of the binomial expansion (a + b)n, which of the following is incorrect ?
Correct Answer: d
Explanation:- The coefficient of terms (x+a)n equidistant from the beginning and the end are equal. These coefficients are known as the binomial coefficients.
nCr = nCn – r, r = 0,1,2,…,n.
The middle term in the expansion of (x + y)10 is the
Number of terms(n) = 10
Middle term = (n/2) + 1
= (10/2) + 1
= 5 + 1
= 6th term
If in the expansion of (1+x)20, the coefficients of rth and (r+4)th terms are equal, then the value of r is equal to:
Coefficients of the rth and (r+4)th terms in the given expansion are Cr−120 and 20Cr+3.
Here,Cr−120 = 20Cr+3
⇒ r−1+r+3 = 20
[∵ if nCx = nCy ⇒ x = y or x+y = n]
⇒ r = 2 or 2r = 18
⇒ r = 9
The number of terms in the expansion of (x – y + 2z)7 are:
Here the number of terms can be calculated by:
= ((n+ 1) * (n+2)) /2
where, n =7
∴ Number of terms = 36
The number of terms in the expansion of (a + b + c)n are:
No. of terms is n+2C2
The general term in the expansion of (a - b)n is
If a and b are real numbers and n is a positive integer, then:
(a - b)n = nC0 an + nC1 a(n – 1) b1 + nC2 a(n – 2) b2+ ...... + nCr a(n – r) br+ ... + nCnbn,
The general term or (r + 1)th term in the expansion is given by:
Tr + 1 = (-1)Cr a(n–r) br
|
156 videos|176 docs|132 tests
|
|
Use Code STAYHOME200 and get INR 200 additional OFF
|
Use Coupon Code |
|
156 videos|176 docs|132 tests
|
Download free EduRev App
Related content with Test: Binomial Theorem For Positive Index
|
|
|
|
Related tests with Test: Binomial Theorem For Positive Index
|
|
|
|
|
|
© EduRev
|
Education Revolution
|
Follow Us
|
