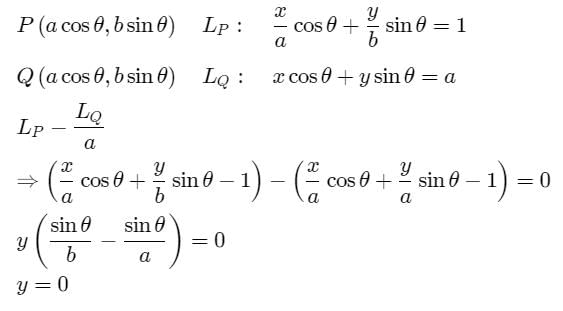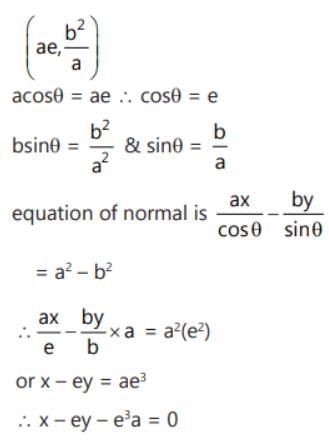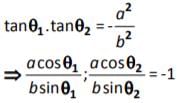Test: Ellipse- 2 - Commerce MCQ
20 Questions MCQ Test Mathematics (Maths) Class 11 - Test: Ellipse- 2
If distance between the directrices be thrice the distance between the foci, then eccentricity of ellipse is
If the eccentricity of an ellipse be 5/8 and the distance between its foci be 10, then its latus rectum is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The curve represented by x = 3(cost + sint), y = 4(cost – sint), is
If the distance of a point on the ellipse +
= 1 from the centre is 2, then the eccentric angle is
An ellipse having foci at (3, 3) and (–4, 4) and passing through the origin has eccentricity equal to
A tangent having slope of - 4/3 to the ellipse +
= 1 intersects the major & minor axes in points A & B respectively. If C is the centre of the ellipse then the area of the triangle ABC is
The equation to the locus of the middle point of the portion of the tangent to the ellipse +
= 1 included between the co-ordinate axes is the curve
An ellipse is drawn with major and minor axes of lengths 10 and 8 respectively. Using one focus as centre, a circle is drawn that is tangent to the ellipse, with no part of the circle being outside the ellipse. The radius of the circle is
Which of the following is the common tangent to the ellipses +
= 1 &
+
= 1 ?
Angle between the tangents drawn from point (4, 5) to the ellipse +
= 1 is
The eccentricity of the ellipse +
= 1 is decreasing at the rate of 0.1/second due to change in semi minor axis only. The time at which ellipse become auxiliary circle is
The point of intersection of the tangents at the point P on the ellipse +
= 1, and its corresponding point Q on the auxiliary circle meet on the line
Q is a point on the auxiliary circle of an ellipse. P is the corresponding point on ellipse. N is the foot of perpendicular from focus S, to the tangent of auxiliary circle at Q. Then
Q is a point on the auxiliary circle corresponding to the point P of the ellipse +
= 1. If T is the foot of the perpendicular dropped from the focus S onto the tangent to the auxiliary circle at Q then the D SPT is
The equation of the normal to the ellipse +
= 1 at the positive end of latus rectum is
The eccentric angle of the point where the line, 5x - 3y = 8√2 is a normal to the ellipse +
= 1 is
PQ is a double ordinate of the ellipse x2+ 9y2 = 9, the normal at P meets the diameter through Q at R, then the locus of the mid point of PR is
If F1 & F2 are the feet of the perpendiculars from the foci S1 & S2 of an ellipse +
= 1 on the tangent at any point P on the ellipse, then (S1F1) . (S2F2) is equal to
If tan q1. tan q2 = – then the chord joining two points q1 & q2 on the ellipse
+
= 1 will subtend a right angle at
|
75 videos|238 docs|91 tests
|
|
75 videos|238 docs|91 tests
|