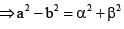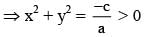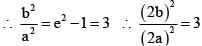Test: Hyperbola- 2 - Commerce MCQ
30 Questions MCQ Test Mathematics (Maths) Class 11 - Test: Hyperbola- 2
If the tangent at the point (h, k) on the hyperbola 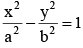 meets the auxiallary circle of the hyperbola in two points whose ordinates y1, y2 then
meets the auxiallary circle of the hyperbola in two points whose ordinates y1, y2 then 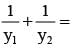
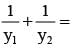
If x = 9 is the chord of contact of the hyperbola x2 - y2 = 9, then the equation of the tangent at one of the points of contact is
Equation of the chord of the hyperbola 25x2 - 16y2 = 400, which is bisected at the point (6, 2) is
The mid-point of the chord 4x – 3y = 5 of the hyperbola 2x2 - 3y2 = 12 is
The equation of the transverse and conjugate axes of a hyperbola are respectively x + 2y – 3 = 0, 2x – y + 4 = 0 and their respective lengths are √2 and 2/√3. The equation of the hyperbola is
If two distinct tangents can be drawn from the point (α,2) on different branches of the hyperbola
A hyperbola has centre C and one focus at P(6, 8). If its two directrices are 3x + 4y + 10 = 0 and 3x + 4y -10 = 0 then CP =
A hyperbola, having the transverse axis of length 2 sin θ, is confocal with the ellipse 3x2 + 4y2 = 12. Then its equation is:
Consider a branch of the hyperbola x2 - 2y2 - 2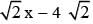 y - 6 = 0 with vertex at the point A. Let B be one of the end points of its latus rectum. If C is the focus of the hyperbola nearest to the point A, then the area of the triangle ABC is
y - 6 = 0 with vertex at the point A. Let B be one of the end points of its latus rectum. If C is the focus of the hyperbola nearest to the point A, then the area of the triangle ABC is
If α + β = 3π then the chord joining the points 'a' and 'b' for hyperbola passes through
The number of tangents and normals to the hyperbola of the slope 1 is
From any point on the hyperbola tangents are drawn to the hyperbola
The area cut off by the chord of contact on the asymptotes is equal to
If the line ax + by + c = 0 is a normal to the hyperbola x y = 1, then
A tangent to the parabola x2 = 4ay meets the hyperbola x2 - y2 = a2 at two points P and Q, then midpoint of P and Q lies on the curve
The point of intersection of two tangents to the hyperbola x2/a2 – y2/b2 = 1, the product of whose slopes is c2, lies on the curve.
Let P(a secθ, b tanθ) and Q(a secφ, b tanφ) where θ+φ = π/2, be two points on the hyperbola 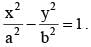 If (h, k) is the point of the intersection of the normals at P and Q, then k is equal to
If (h, k) is the point of the intersection of the normals at P and Q, then k is equal to
Foot of normals drawn from the point p(h,k) to the hyperbola will always lie on the conic
A variable chord PQ, x cos θ + y sin θ = P of the hyperbola subtends a right angle at the origin. This chord will always touch a circle whose radius is
If the equation 4x2 + ky2 = 18 represents a rectangular hyperbola, then k =
The locus of the point of intersection of tangents drawn at the extremities of normal chords to hyperbola xy = c2
The equation of a line passing through the centre of a rectangular hyperbola is x – y –1 = 0. if one of its asymptote is 3x-4y-6 = 0, then equation of its other asymptote is
Tangents are drawn to 3x2 - 2y2 = 6 from a point P. If these tangents intersects the coordinate axes at concyclic points, The locus of P is
Let a and b be non–zero real numbers. Then, the equation (ax2 + by2 + (C) (x2 – 5xy + 6y2) = 0 represents
The asymptotes of the curve 2x2 + 5xy + 2y2 + 4x + 5y = 0 are given by
A hyperbola passing through origin has 3x – 4y – 1 = 0 and 4x – 3y – 6 = 0 as its asymptotes. Then the equation of its transverse axis is
If the vertex of a hyperbola bisects the distance between its centere and the corresponding focus, then ratio of square of its conjugate axis of the square of its transverse axis is
|
75 videos|238 docs|91 tests
|


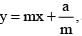 a = 2 and c2 = a2m2 - b2
a = 2 and c2 = a2m2 - b2
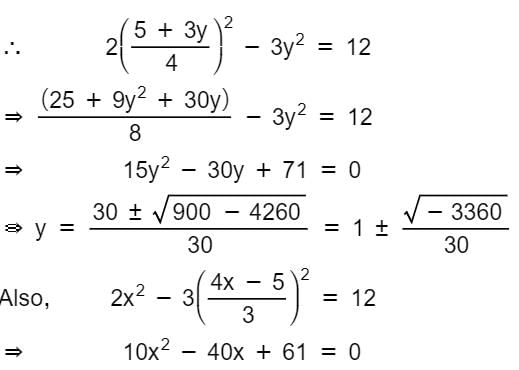
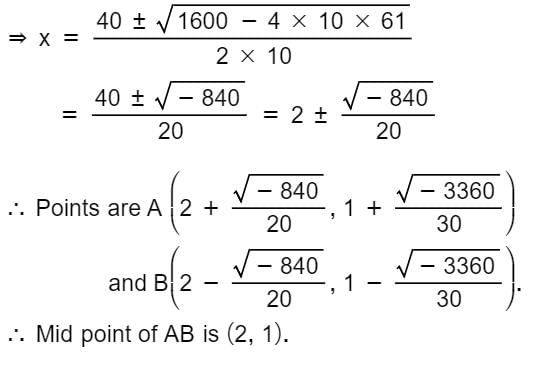

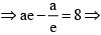
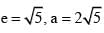
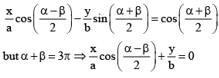
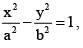
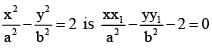
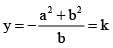
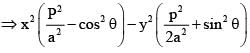
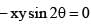
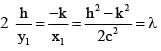
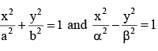 cut each other orthogonally then
cut each other orthogonally then 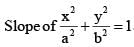
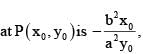
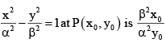
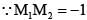
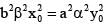 ------(1)
------(1)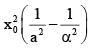
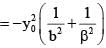 -------(2)
-------(2)