Test: Introduction To Vector Algebra - JEE MCQ
20 Questions MCQ Test Mathematics (Maths) for JEE Main & Advanced - Test: Introduction To Vector Algebra
For what values of x and y, the vectors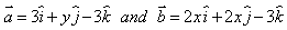 are equal?
are equal?
Two or more vectors having the same initial point are called
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If the magnitude of the position vector is 7, the value of x is:
If 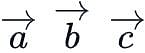 and
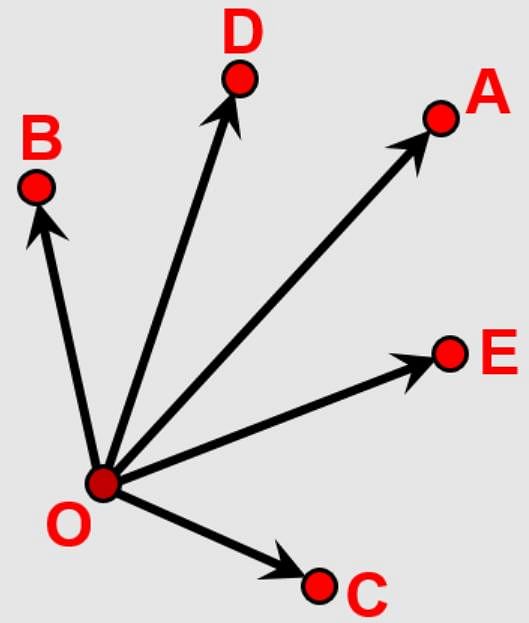
and 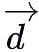 are the position vectors of the points A, B, C and D such that
are the position vectors of the points A, B, C and D such that 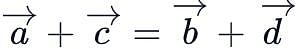 then ABCD is:
then ABCD is:
The angles α, β, γ made by the vector with the positive directions of X, Y and Z-axes respectively, then the direction cosines of the vector
are:
If a and b are the position vectors of two points A and B and C is a point on AB produced such that AC = 3AB, then position vector of C will be
If and
, then the value of scalars x and y are:
The unit vector in the direction of , where A and B are the points (2, – 3, 7) and (1, 3, – 4) is:
A vector of magnitude 14 units, which is parallel to the vector
For any two vectors a and b, we always have
If l, m, n are the direction cosines of a position vector 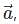 then which of the following is true?
then which of the following is true?
A vector whose initial and terminal points coincide, is called
A point from a vector starts is called______and where it ends is called its______.
If are position vectors of the points (- 1, 1) and (m, – 2). then for what value of m, the vectors
are collinear.
|
209 videos|443 docs|143 tests
|
|
209 videos|443 docs|143 tests
|



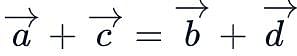
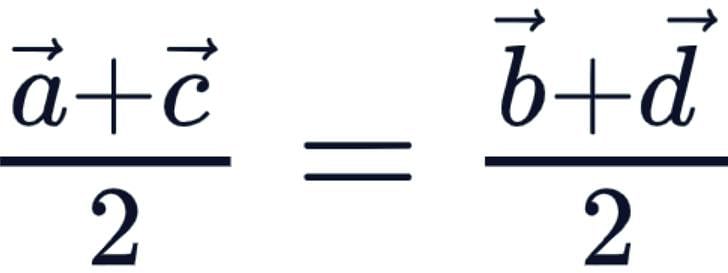


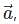 is the position vector of a point M(x,y,z) and α, β, γ are the angles, made by the vector
is the position vector of a point M(x,y,z) and α, β, γ are the angles, made by the vector 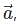 with the positive directions of x, y and z respectively. The cosines of the angles, cosα, cosβ, cosγ are the direction cosines of the vector
with the positive directions of x, y and z respectively. The cosines of the angles, cosα, cosβ, cosγ are the direction cosines of the vector 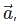 denoted by l, m, n, then
denoted by l, m, n, then














