Test: Matrices- 1 - JEE MCQ
25 Questions MCQ Test Mathematics (Maths) Class 12 - Test: Matrices- 1
The number of all possible matrices of order 3×3 with each entry 0 if 1 is
Two matrices A and B are multiplicative inverse of each other only if
For what value of λ the following system of equations does not have a solution ? x + y + z = 6, 4x + λy - λz = 0, 3 x + 2y – 4 z = - 5
If A and B are square matrices of the same order, then(A+B)2 = A2+2AB+B2 implies
The value of λ, for which system of equations. x + y + z = 1, x + 2y + 2z = 3, x + 2y + λz = 4, have no solution is
If P is of order 2 × 3 and Q is of order 3 × 2, then PQ is of order
A square matrix A = [aij]n×n is called a lower triangular matrix if aij = 0 for
The transformation ‘orthogonal projection on X-axis’ is given by the matrix
The number of all the possible matrices of order 2 × 2 with each entry 0, 1 or 2 is
A square matrix A = [aij]n×n is called an upper triangular if aij = 0 for
The equations, x + 4 y – 2 z = 3, 3 x + y + 5 z = 7, 2 x + 3y +z = 5 have
If the system of equationsx + 4 ay + az = 0, x + 3by + bz = 0 andx + 2 cy +cz = 0 have a non-zero solution,then a, b, c are in
|
204 videos|290 docs|139 tests
|



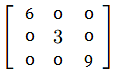

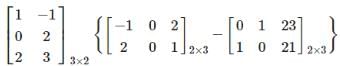
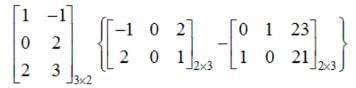
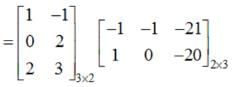
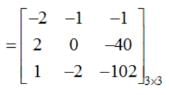
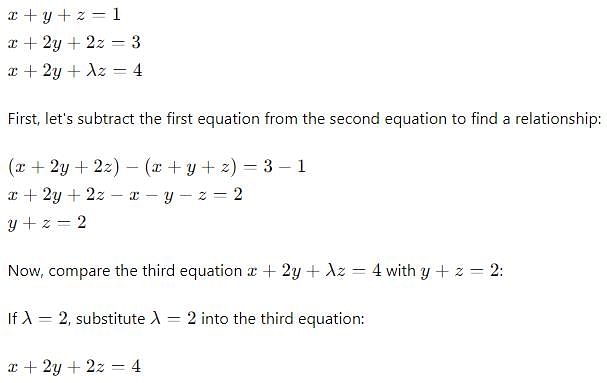
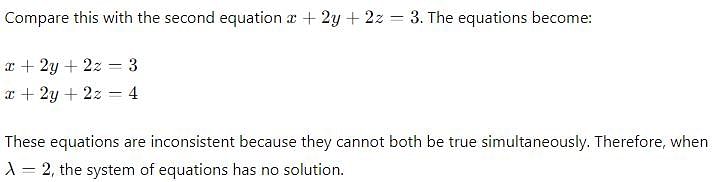

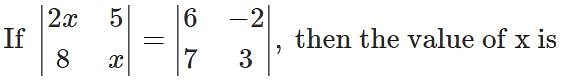
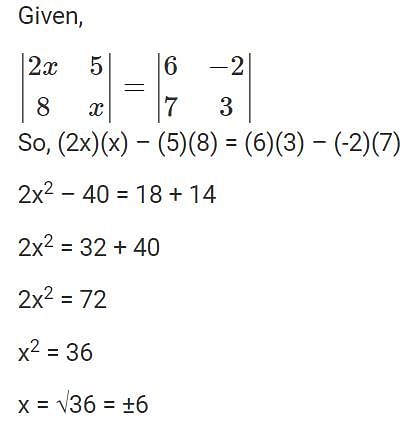
 ,
,
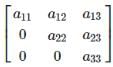 .
.
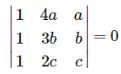
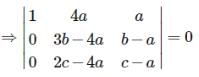
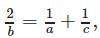 ∴ there, a , b ,c, are in H.P
∴ there, a , b ,c, are in H.P














