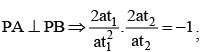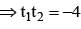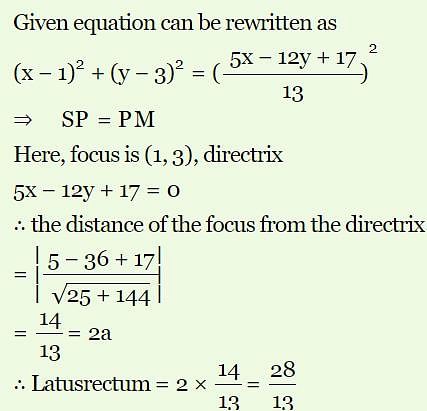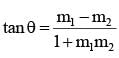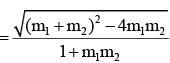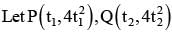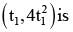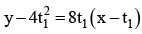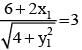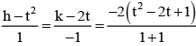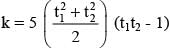Test: Parabola- 3 - JEE MCQ
30 Questions MCQ Test Mathematics (Maths) for JEE Main & Advanced - Test: Parabola- 3
The combined equation to two parabolas, both have their axis along x-axis, is given by y4 - y2 (4x + 4 - 2 sin22α) + sin22α (4x + 4x + sin2 2α) = 0. The locus of the point of intersection of tangents, one to each of the parabolas, when they include an angle of 90°
is
is
The straight line x + y = k + 1 touches the parabola y = x(1 – x) if
Focus and vertex of the parabola that touches x-axis at (1, 0) and x = y at (1, 1) are (h, k) and (p, q) then the value of 25(p + q +h + k)
Number of circles that touch a given parabola and one of its fixed focal chords at focus is
The chord AB of the parabola y2 = 4ax cuts the axis of the parabola at C. If 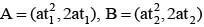 and AC : AB = 1 : 3, then
and AC : AB = 1 : 3, then
For the parabola x2=16y, find the equation of the normal at the point (4,4).
If the parametric equations of the parabola are given by x = 4t2 - 2t + 1; y = 3t2 + t + 1 and the vertex of the parabola also satisfies y - x = k/100, then the area of the circle x2 + y2 + 12x -10y + 2k = 0 in square units is
A parabola has focus at (0, 0) and passes through the points (4, 3) and (–4, –3). The number of lattice points (x, y) on the parabola such that |4x + 3y| < 1000 is
Center of the smallest circle that is drawn to touch the two parabolas given by y2 + 2x + 2y + 3 = 0; x2 + 2x + 2y + 3 = 0 is
The equation of directrix and latusrectum of a parabola are 3x – 4y + 27 = 0 and 3x – 4y + 2 = 0. Then the length of latusrectum is
Let A ≡ (9, 6), B(4, -4) be two points on parabola y2 = 4x and P(t2, 2t), t∈[-2, 3] be a variable point on it such that area of DPAB is maximum, then point P will be
Two tangents to the parabola y2 = 4x, one drawn at a point P and another drawn at the point where the normal at the image of P in the axis of the parabola meets the curve again, include an angle
If the chord joining the points t1 and t2 on the parabola y2 = 4ax subtends a right angle at its vertex then t2 =
The equation of the latusrectum of the parabola y2 – 6y + 4x – 3 = 0 is
The equation of the latusrectum of the parabola y2 – 6y + 4x – 3 = 0 is
If the line x – 1 = 0 is the directrix of the parabola y2 – kx + 8 = 0, then one of the value of k is
The curve described parametrically by x = t2 + t + 1, y = t2 - t + 1 represents
The length of the latus rectum of the parabola 169{(x - 1)2 + (y - 3)2} = (5x - 12y + 17)2} is
The angle between the tangents drawn from the point (3, 4) to the parabola y2 - 2y + 4x = 0 is
Equation of common tangent of parabola y2 = 8x and x2 + y = 0 is
If the tangents at two points (1, 2) and (3, 6) as a parabola intersect at the point (– 1, 1), then the slope of the directrix of the parabola is
A variable chord PQ of the parabola y = 4x2 substends a right angle at the vertex. Then the locus of points of intersection of the tangents at P and Q is
Point on the curve y2 = 4(x- 10) which is nearest to the line x + y = 4 may be
If (h, k) is a point on the axis of parabola 2(x -1)2 + 2 (y -1)2 = (x + y + 2)2 from where three distinct normals can be drawn, then
The equation of the common tangent touching the circle (x – 3)2 + y2 = 9 and the parabola y2 = 4x below y2 - 4x below the x–axis is
The line x + y = 6 is a normal to the parabola y2 = 8x at the point
The tangent and normal at the point P(4, 4) to the parabola, y2 = 4x intersect the x–axis at the points Q and R respectively. Then the cirucm centre of the ΔPQR is
All chords of the parabola y2 = 4x which subtend right angle at the origin are concurrent at the point:
The mirror image of the parabola y2 = 4x in the tangent to the parabola to the point (1,2) is
The locus of mid–point of family of chords λx + y - 5 = 0 (parameter) of the parabola x2 = 20y is
|
209 videos|443 docs|143 tests
|
|
209 videos|443 docs|143 tests
|


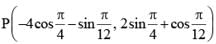 as origin and line joining it to the centre as x-axis, the equation to the circle becomes x2 + y2 - 2x = 0, center is A1 (1, 0) and the second circle has the equation x2 + y2 - 2√2 = 0 center A0 (0, √2)
as origin and line joining it to the centre as x-axis, the equation to the circle becomes x2 + y2 - 2x = 0, center is A1 (1, 0) and the second circle has the equation x2 + y2 - 2√2 = 0 center A0 (0, √2)
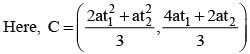
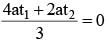

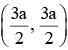
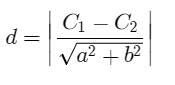
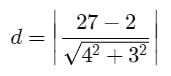
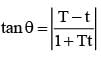
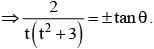
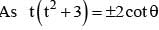 can have only one real root, there will be only one such point P.
can have only one real root, there will be only one such point P.