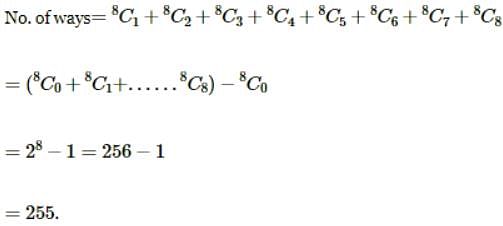Test: Permutations And Combinations - 2 - Commerce MCQ
25 Questions MCQ Test Mathematics (Maths) Class 11 - Test: Permutations And Combinations - 2
A fair dice is rolled n times. The number of all the possible outcomes is
The sum of all the numbers which can be formed by using the digits 1,3,5,7 all at a time and which have no digit repeated, is
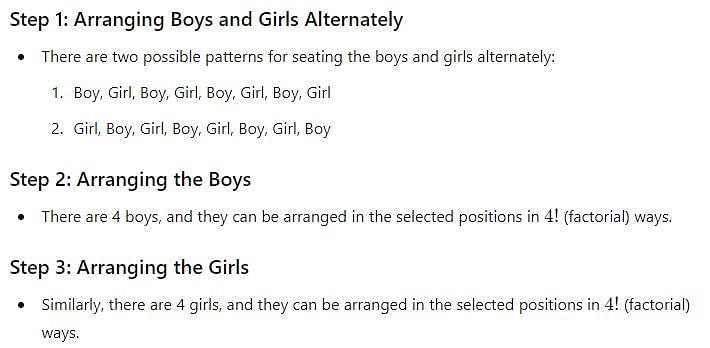
4 boys and 4 girls are to be seated in a row. The number of ways in which this can be done, if the boys and girls sit alternately, is
The letters of the word ‘SOCIETY’ are arranged in such a manner that the vowels and consonants occur alternately, the number of different words so obtained is
There are 10 true-false questions. The number of ways in which they can be answered is [ it is must to attempt the question ]
The number of ways in which 6 “ + “ and 4 “ – “ signs can be arranged in a line such that no two “ – “ signs occur together is
On a railway track, there are 20 stations. The number of tickets required in order that it may be possible to book a passenger from every station to every other is
A class is composed 2 brothers and 6 other boys. In how many ways can all the boys be seated at the round table so that the 2 brothers are not seated besides each other?
The number of all selections which a student can make for answering one or more questions out of 8 given questions in a paper, when each question has an alternative, is:
The number of ways in which 8 different flowers can be strung to form a garland so that 4 particular flowers are never separated is
Different calendars for the month of February are made so as to serve for all the coming years. The number of such calendars is
The number of all odd divisors of 3600 is
The number of all even divisors of 1600 is
A convex polygon of n sides has n diagonals. The value of n is
The number of all possible positive integral solutions of the equation xyz = 30 is
Number of all 4 digit numbers with distinct digits is
The number of ways, in which a student can choose 5 courses out of 8 courses, when 2 courses are compulsory, is
An online examination have 12 question out of which we havethe alternative to select the answer. Choose how many ways can be there in which one can answer the question
20 students can compete for a race. The number of ways in which they can win the first three places is (given that no two students finish in the same place)
The number of ways of dividing 52 cards equally into 4 sets is
The number of three digit numbers having atleast one digit as 5 is
5 boys and 5 girls are to be seated around a table such that boys and girls sit alternately. The number of ways of seating them is
The total number of numbers from 1000 to 9999 (both inclusive) that do not have 4 different digits
|
75 videos|238 docs|91 tests
|