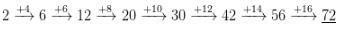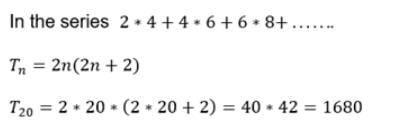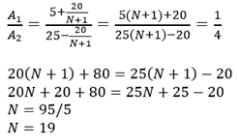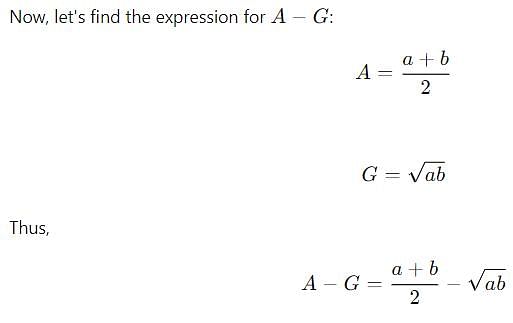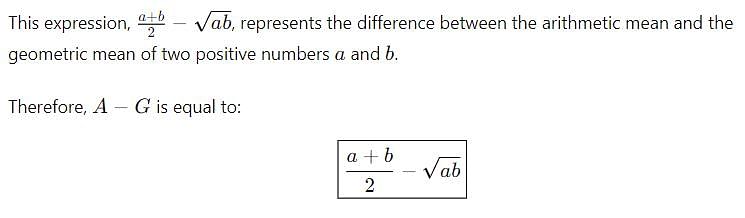Test: Sequence and Series - Commerce MCQ
25 Questions MCQ Test Mathematics (Maths) Class 11 - Test: Sequence and Series
Which term of the sequence 8 – 6i, 7 – 4i, 6 – 2i, ….is a real number ?
All the terms in A.P., whose first term is a and common difference d are squared. A different series is thus formed. This series is a
If a, 4, b are in A.P.; a, 2, b are in G.P.; then a, 1, b are in
The eleventh term of the sequence 1, 1, 2, 3, 5, 8, 13, 21, 34, ….. is
In an A.P., sum of first p terms is equal to the sum of first q terms. Sum of its first p + q terms is
The sum of 40 A.M.’s between two number is 120. The sum of 50 A.M.’s between them is equal to
In an A.P., sum of first p terms is q and sum of first q terms is p. Sum of its p + q terms is
pth term of an A.P. is q and qth term is p, its (p+ q)th term is
pth term of an H.P. is qr and qth term is pr, then rth term of the H.P. is
The value of b for which the roots of the equation sin x = b are in A.P. is
The number of numbers between n and n2 which are divisible by n is
The number of terms common to the Arithmetic progressions 3, 7, 11, …., 407 and 2, 9, 16, …., 709 is
The ratio of first to the last of n A.m.’s between 5 and 25 is 1 : 4. The value of n is
If A, G, H denote respectively the A.M., G.M. and H.M. between two unequal positive quantities then
If A, G and H denote respectively, the A.M., G.M. and H.M. between two positive numbers a and b, then A - G is equal to
The sum of all 2-digited numbers which leave remainder 1 when divided by 3 is
The number of numbers between 105 and 1000 which are divisible by 7 is
|
75 videos|238 docs|91 tests
|