Test: Sets - Commerce MCQ
25 Questions MCQ Test Mathematics (Maths) Class 11 - Test: Sets
Consider the following statements:
I: If A = {x: x is an even natural number} and B = {y: y is a natural number}, A subset B.
II: Number of subsets for the given set A = {5, 6, 7, 8) is 15.
III: Number of proper subsets for the given set A = {5, 6, 7, 8) is 15.
Which of the following statement(s) is/are correct?
Let A and B be two finite sets having m and n elements, respectively. Then the total number of mapping from A to B is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Consider the following relations:
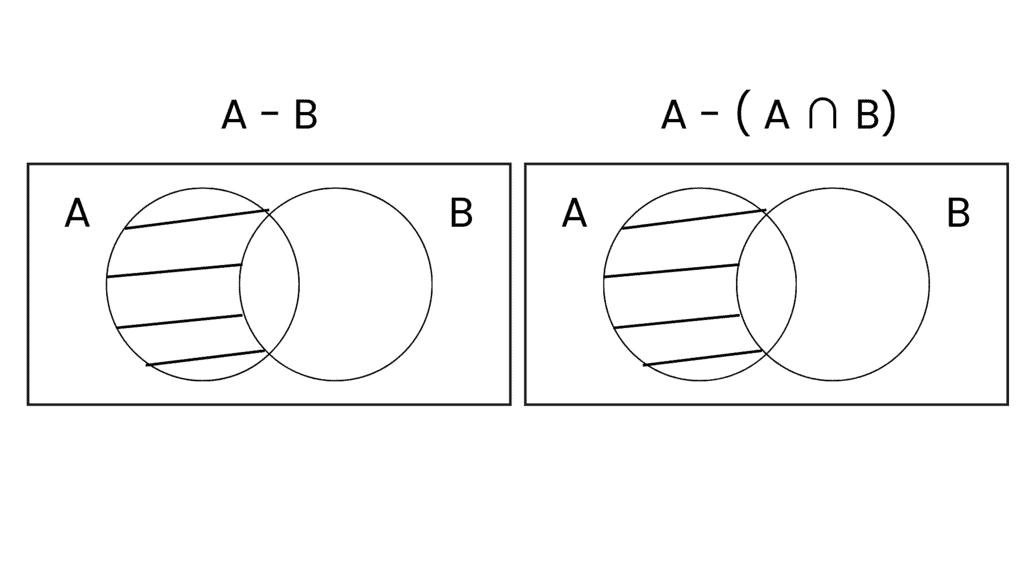
(i) A - B = A - (A ∩ B)
(ii) A = (A ∩ B) ∪ (A - B)
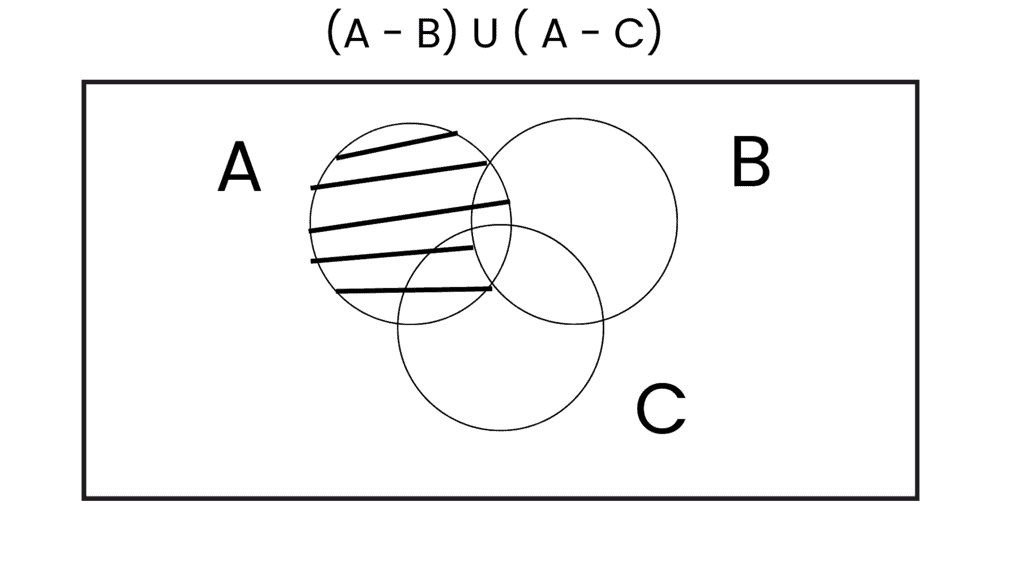
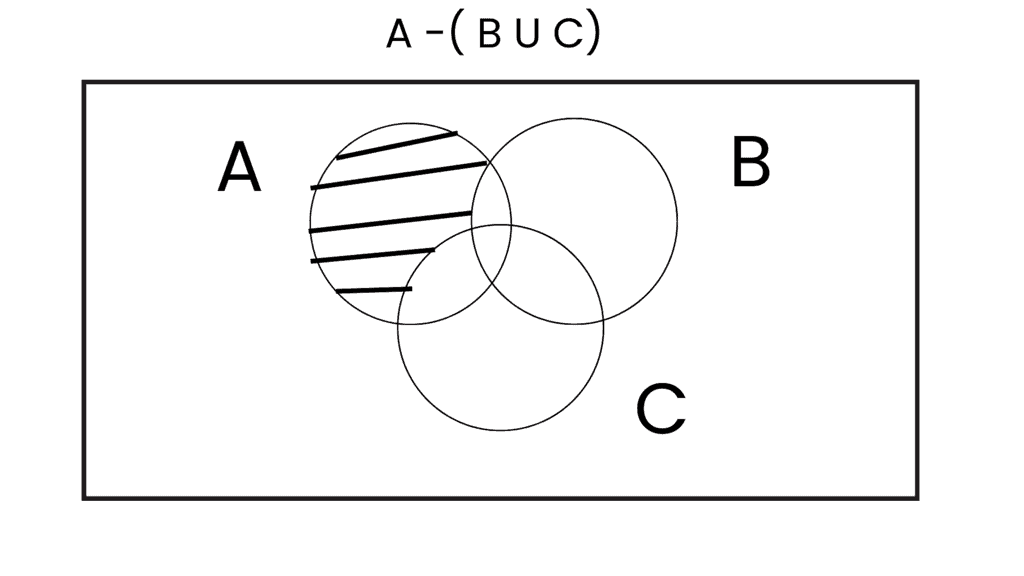
(iii) A - (B ∪ C) = (A - B) ∪ (A - C)
Which of these is/are correct?
(i) A - B = A - (A ∩ B)
(ii) A = (A ∩ B) ∪ (A - B)
(iii) A - (B ∪ C) = (A - B) ∪ (A - C)
Which of these is/are correct?
Two sets, A and B, are as under:
A = {(a, b) ∈ R × R : |a − 5| < 1 and |b − 5| < 1};
B = {a, b) ∈ R × R : 4 (a − 6)2 + 9(b−5) 2 ≤ 36}. Then,
Let A and B be two sets containing 4 and 2 elements, respectively. Then the number of subsets of the set AxB, each having at least 3 elements, is
In a city, 20 per cent of the population travels by car, 50 per cent travels by bus and 10 per cent travels by both car and bus. Then persons travelling by car or bus is:
Let U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, A = {1, 2, 5}, B = {6, 7}. Then A ∩ B’ is:
If A = {2, 3, 4, 8, 10}, B = {3, 4, 5, 10, 12}, C = {4, 5, 6, 12, 14} then (A ∩ B) ∪ (A ∩ C) is equal to:
Let A and B be two sets containing four and two elements respectively.Then the number of subsets of the set A × B,each having atleast three elements is:
The number of elements in the set {(a, b) : 2a2 + 3b2 = 35, a, b ∈ Z}, where Z is the set of all integers, is:
Given n(U) = 20, n(A) = 12, n(B) = 9, n(A ∩ B) = 4, where U is the universal set, A and B are subsets of U, then n((A ∪ B)c) =
In a certain town, 25% families own a cell phone,15% families own a scooter and 65% families own neither a cell phone nor a scooter. If 1500 families own both a cell phone and a scooter, then the total number of families in the town is:
If A = {2, 3, 4, 8, 10}, B = {3, 4, 5, 10, 12} and C = {4, 5, 6, 12, 14}, then (A∩B)∪(A∩C) is equal to:
If n(A) = 3, n(B) = 6 and A ⊆ B. Then the number of elements in A ∪ B is equal to:
In a class of 100 students, 55 students have passed in Mathematics and 67 students have passed in Physics. Then the number of students who have passed in Physics only is:
|
75 videos|238 docs|91 tests
|
|
75 videos|238 docs|91 tests
|