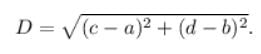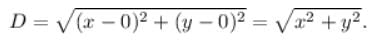Test: Straight Lines- 1 - JEE MCQ
25 Questions MCQ Test Mathematics (Maths) for JEE Main & Advanced - Test: Straight Lines- 1
The point which divides the joint of (1, 2) and (3,4) externally in the ratio 1 : 1.
The line through the points (a , b) and (- a, - b) passes through the point
Projection (the foot of perpendicular) from (x , y) on the x – axis is
The distance between the lines 5x – 12y + 65 = 0 and 5x – 12y – 39 = 0
The equation y−y1 = m (x−x1), m ∈ R, represents all lines through the point (x1,y1) except the line
The distance between the parallel lines 3x + 4y + 13 = 0 and 3x + 4y – 13 = 0 is
The straight lines x + y = 0 , 3x + y – 4 = 0 , x + 3y – 4 = 0 form a triangle which is
The equation of the line which passes through the point (1 , - 2) and cuts off equal intercepts from the axis is
If a line is drawn through the origin and parallel to the line x – 2y + 5 = 0 , its equation is
The line passing through (1, 1) and parallel to the line 2x – 3y + 5 = 0 is
The equation of the line which passes through the point (2 , - 3) and cuts off equal intercepts from the axis is
The vertex A of a triangle ABC is the point (-2, 3) whereas the line perpendicular to the sides AB and AC are x – y – 4 = 0 and 2x – y – 5 = 0 respectively. The right bisectors of sides meet at P(3/2 , 5/2) . Then the equation of the median of side BC is
The distance between the lines 4x + 3y = 11 and 8x + 6y = 15 is ?
The line which passes through the point (0 , 1) and perpendicular to the line x – 2y + 11 = 0 is
Thee perpendicular distance of the origin from the line 3x +4y + 1 = 0 is
The vertices of a triangle are (0 , 3) , (- 3 , 0) and (3 , 0). The orthocenter of the triangle is
|
176 videos|582 docs|160 tests
|
|
176 videos|582 docs|160 tests
|