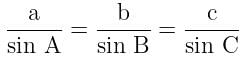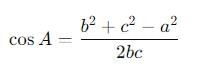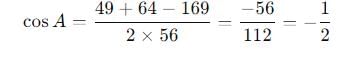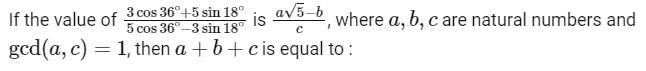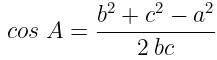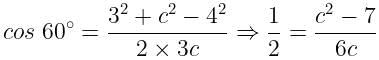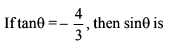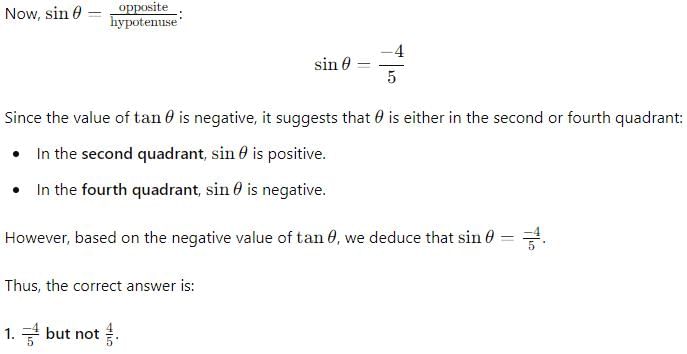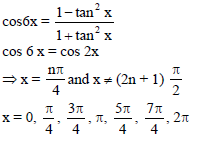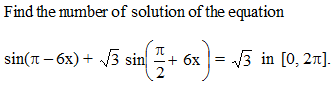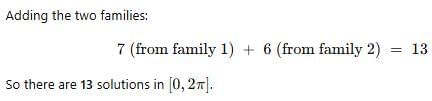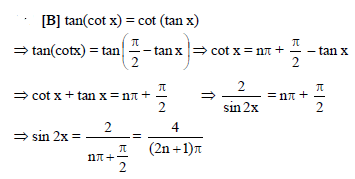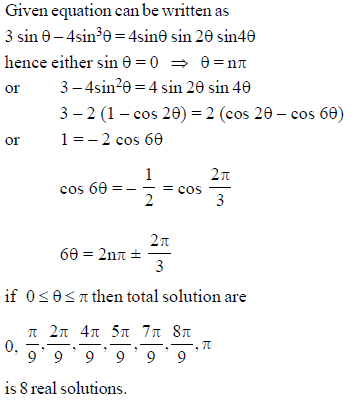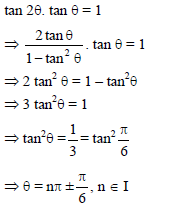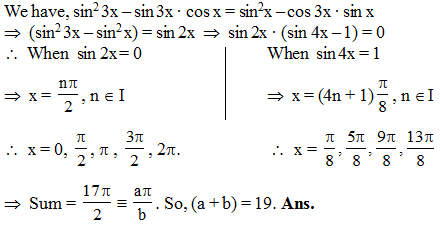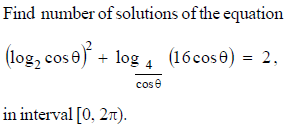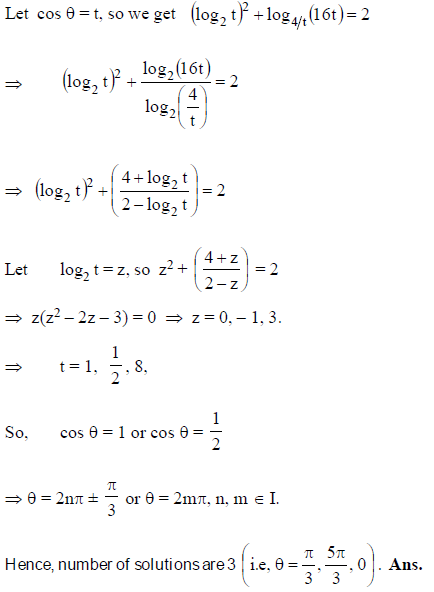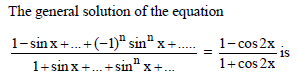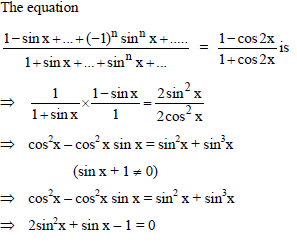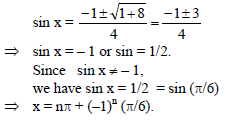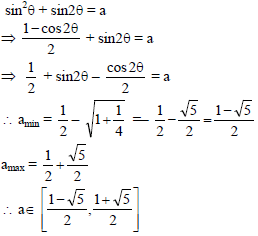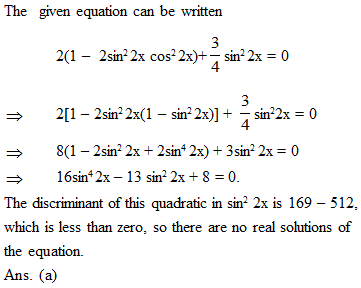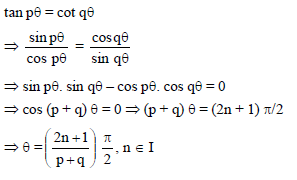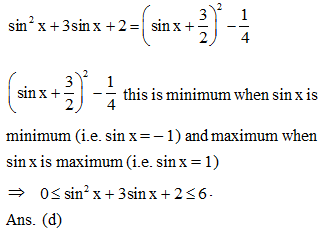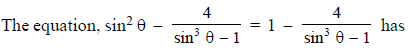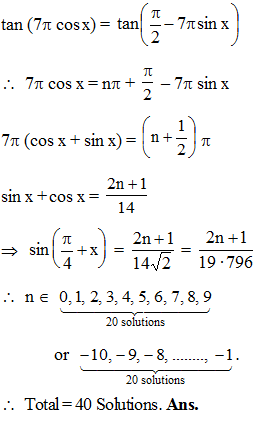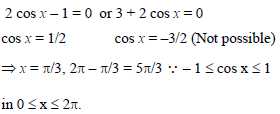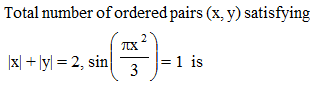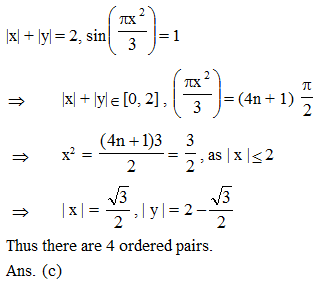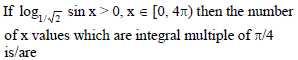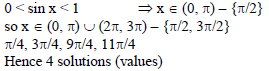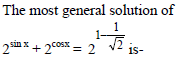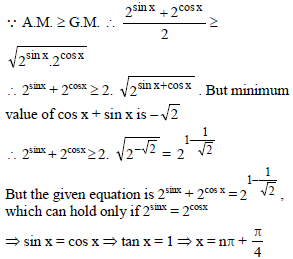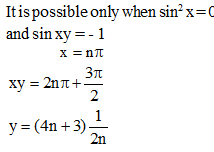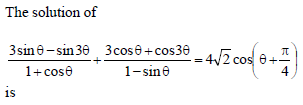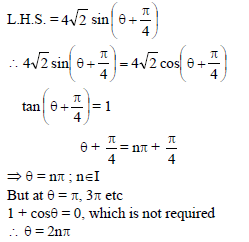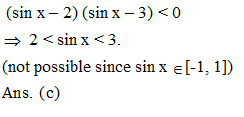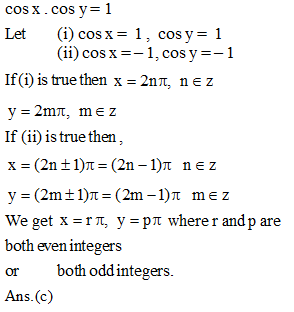Trigonometric Ratios, Functions & Equations - 1 - JEE MCQ
30 Questions MCQ Test - Trigonometric Ratios, Functions & Equations - 1
The angles of a triangle are as 1 : 2 : 7, then ratio of greatest side to least side is
If the sides of a triangle are 13, 7, 8 the greatest angle of the triangle is
If a = 4, b = 3 and A = 60∘, then c is a root of the equation
If cos A + cos B = , then the sides of the triangle ABC are in
Number of solutions of the equation cos6x + tan2x + cos6x . tan2x = 1 in the interval [0, 2π] is-
If tan(cot x) = cot(tan x), then sin 2x =
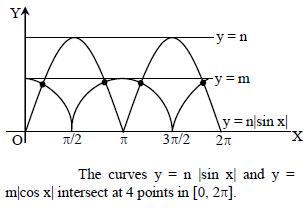
If m and n(> m) are positive integers, the number of solutions of equation n|sin x| = m|cos x| in [0, 2π] is -
sin 3 θ = 4 sin θ sin 2 θ sin 4 θ in 0 ≤ θ ≤ π has
The general solution to the equation tan 2θ. tan θ = 1 is
The number of pairs (x, y) satisfying the equations sin x + sin y = sin(x + y) and | x | + | y | = 1 is
If the equation sin θ (sin θ + 2 cos θ) = a has a real solution, then the shortest interval containing all possible values of ‘a’ is
The number of solutions of the equation 2(sin4 2x + cos4 2x) + 3 sin2 x cos2 x = 0 is
Solution to the equation tan pθ = cot qθ is
Find the number of principal solution of the equation tan (7π cos x) = cot (7π sin x).
The solution set of (2 cos x– 1) (3 + 2 cos x) = 0 in the interval 0 ≤ x ≤ 2π is -
If sin2 x + sin xy = – 1, then the value of x, y is
Solution of the inequality sin2x – 5sinx + 6 < 0 is
If cos x . cos y = 1, then the value of x and y is