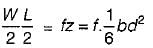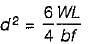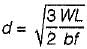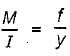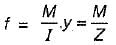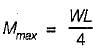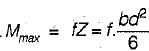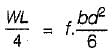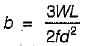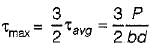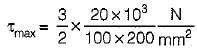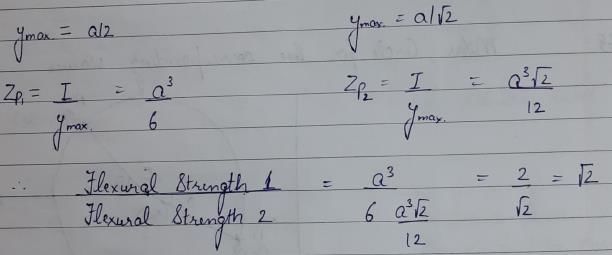Test: Bending & Shear Stress - 1 - Civil Engineering (CE) MCQ
10 Questions MCQ Test GATE Civil Engineering (CE) 2025 Mock Test Series - Test: Bending & Shear Stress - 1
A simply supported beam of span L carries a concentrated load W at its mid-span. If the width b of the beam is constant and its depth is varying throughout the span, then what should be its mid-span depth, when design stress is f?
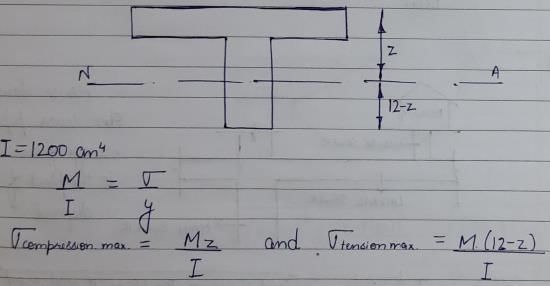
A beam of T-section has I = 1200 cm4 and depth = 12 cm. Flange of the section is in compression. If the maximum tensile stress is two times the maximum compressive stress, what is section modulus in compression?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The width of a beam of uniform strength having a constant depth d, length L, simply supported at the ends with a central load W is
A beam of rectangular cross-section is 100 mm wide and 200 mm deep. If the section is subjected to a shear force of 20 kN, the maximum shear stress is
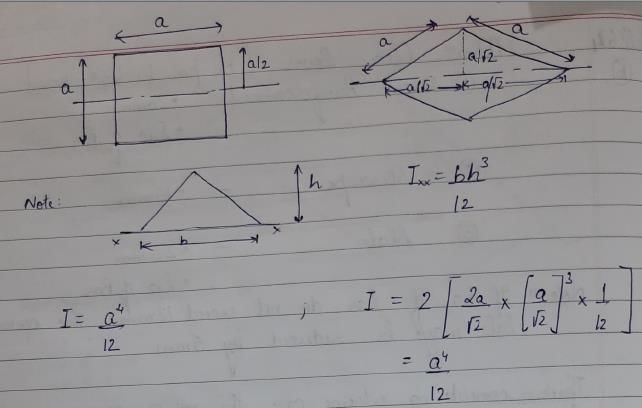
The ratio of the flexural strengths of two square beams one placed with two sides horizontal and the other placed with one diagonal vertical and other horizontal is
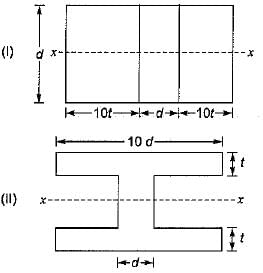
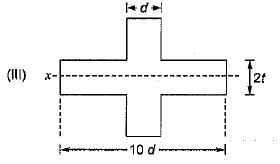
The modular ratio of the materials used in the flitched beam is 10 and the ratio of the allowable stresses is also 10. Four different sections of the beam are: shown in the given figures. The material shown hatched has larger modulus of elasticity and allowable stress than the rest.
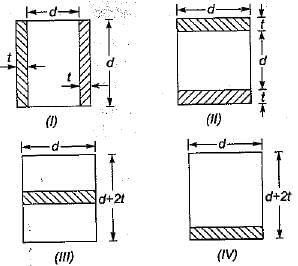
Which one of the following statements is true for the beam under consideration ?
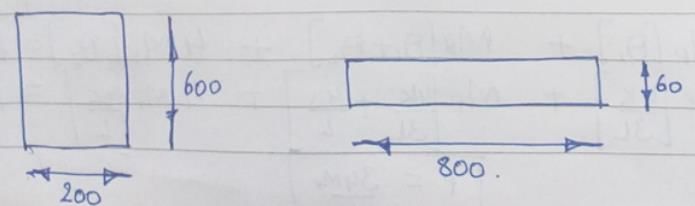
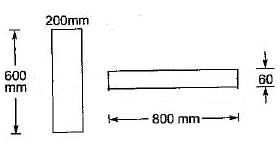
Cross-sections of two beams A (600 mm x 200mm) and B (800 mm x 60 mm) are shown in the figure given above. Both the beams have the same material. By how many times is the beam A stronger than the beam B in resisting bending
A beam of uniform strength refers to which one of the following?
Maximum shear stress in a circular cross-section is
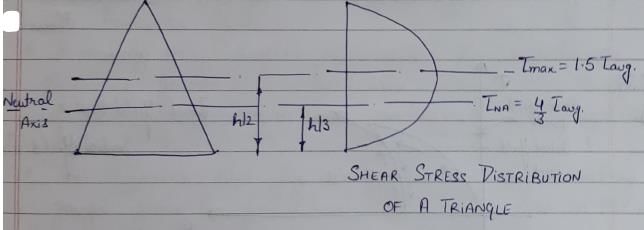
Shear stress in a beam having triangular cross-section is maximum at
|
31 docs|280 tests
|
|
31 docs|280 tests
|