Test: Thin Cylinder Level - 3 - Mechanical Engineering MCQ
10 Questions MCQ Test Strength of Materials (SOM) - Test: Thin Cylinder Level - 3
A thin cylindrical shell made of steel, of diameter 250 mm, wall thickness 6 mm, length 1 m is subjected to internal pressure p such that maximum stress developed in the shell is 120 MPa. If E = 200 GPa and Poisson’s ratio is 0.3. The change in volume of the shell is ___________ cm3
Match List-I with List-II and select the correct answer using the code given below the lists.
List-I List –II
(state of stress) (kind of loading)
(a)  1. Combined bending and torsion of circular shaft
1. Combined bending and torsion of circular shaft
(b) 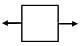 2. Torsion of circular shaft
2. Torsion of circular shaft
(c)  3. Thin cylinder subjected to internal pressure
3. Thin cylinder subjected to internal pressure
(d) 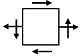 4. Tie bar subjected to tensile force
4. Tie bar subjected to tensile force
Codes: a b c d
 1. Combined bending and torsion of circular shaft
1. Combined bending and torsion of circular shaft 3. Thin cylinder subjected to internal pressure
3. Thin cylinder subjected to internal pressure 4. Tie bar subjected to tensile force
4. Tie bar subjected to tensile force| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
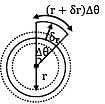
A thin cylinder of radius r and thickness t when subjected to an internal hydrostatic pressure P causes a radial displacement u, then the tangential strain caused is
A bronze cylinder of diameter 200 mm, wall thickness 8 mm is wound with steel wire of diameter 4 mm under initial tension of 20 N/mm2. The wire wound cylinder is subjected to internal pressure p such that resultant hoop and axial stresses developed in the cylinder are the same. What is the magnitude of p? Given Ew = 210 GPa, EC = 105 GPa, νc = 0.35.
Circumferential stress in a cylindrical steel boiler shell under internal pressure is 80MPa. Young’s modulus of elasticity and Poisson’s ratio are respectively 2 × 105 MPa and 0.28. The magnitude of circumferential strain in the boiler shell be
When a thin cylinder of diameter ‘d’ and thickness ‘t’ is pressurized with an internal pressure of ‘p’ (1/m is the Poisson’s ratio and E is the modulus of elasticity), then out of the following, which statement is correct?
A thin walled pressure vessel made of aluminium alloy, 250 mm diameter and 4 mm thick is subjected to an internal pressure of 2.5 N/mm2. Strain gauges mounted on the surface of vessel in circumferential and axial directions give readings of 932 μs and 190 μs respectively, under full pressure, The young’s modulus of the aluminium alloy is _________Gpa
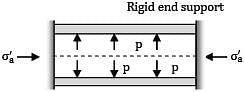
A thin cylindrical shell of diameter 200 mm, thickness 8 mm is held between two rigid supports as shown in figure. An internal pressure of 5 N/mm2 is applied on the inner surface of the cylinder. The resultant axial stresses developed in the cylinder (μ = 0.35) is _________MPa
A closed pressure vessel of diameter 120 mm, wall thickness 4 mm is subjected to an internal pressure of 6 N/mm2. The normal stress on an element of cylindrical wall at 30° to the longitudinal axis of cylinder is __________MPa
A thin cylinder 150 mm internal diameter and 2.5 mm thick has its ends closed by rigid plates and is then filled with water under pressure. When an axial pull of 37 kN is applied to the ends, water pressure is observed to fall by 0.1 N/mm2. The Poisson’s ratio will be (Assume E = 140000 N/mm2, K for water = 2200 N/mm2)
|
37 videos|39 docs|45 tests
|
|
37 videos|39 docs|45 tests
|


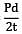 = = 120 N/mm2
= = 120 N/mm2 = 5.76 N/mm2
= 5.76 N/mm2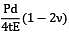

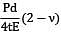


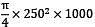


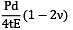
 = 4.905
= 4.905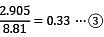
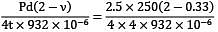
 = 62.5 N/mm2
= 62.5 N/mm2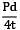 = 31.25 N/mm2
= 31.25 N/mm2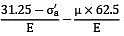 = 0
= 0
 = 90 N/mm2
= 90 N/mm2 =45 N/mm2
=45 N/mm2