Test: Measurements of Area & Volume - 1 - Civil Engineering (CE) MCQ
10 Questions MCQ Test Geomatics Engineering (Surveying) - Test: Measurements of Area & Volume - 1
Which of the following formulas explains the calculation of area of earthwork using its mean depth?
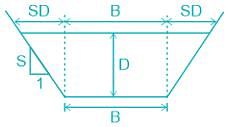
Area = BD + Sd2
Where, B = Breadth of section
D = Mean depth of section
Sd = Areas of sides
Area = BD + Sd2
Where, B = Breadth of section
D = Mean depth of section
Sd = Areas of sides
The formula used to calculate the mean depth of earthwork by averaging the depths of two consecutive sections is called:
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
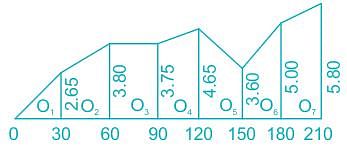
The chainages (m) and corresponding perpendicular offsets(m) taken from a chain line to an irregular boundary were (0, 0), (30, 2.65), (60, 3.80), (90, 3.75), (120, 4.65), (150, 3.60), (180, 5.00) and (210, 5.80). The area (m2) between the chain line and the irregular boundary by Simpson's rule is
For calculation of volume of earthwork, which of the following formulas assumes that short lengths in parabolic arcs are considered as parallel to each other?
Prismoidal correction, while surveying is always?
The sum of first and last ordinates, add twice the sum of the remaining odd ordinates and four times the sum of all the even ordinates. The total sum thus obtained is multiplied by one-third of the common distance between the ordinates and the result gives the required area. This rule of finding the area is called:
The Simpson’s rule for determination of areas is used when the number of offsets are:
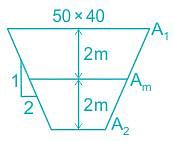
What is the volume of earthwork for constructing a tank that is excavated in the level ground to a depth of 4 m ? The top of the tank is rectangular in shape having an area of 50 m × 40 m and the side slope of the tank is 2: 1 (horizontal: vertical).
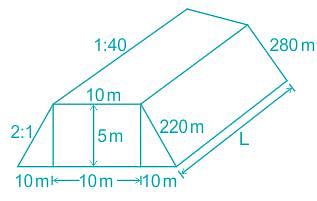
A road embankment 10 m wide at the formation level with side slopes 2:1 and with an average height of 5 m is constructed with an average gradient of 1:40 from the contour 220 m to 280 m. Find the volume of earthwork.
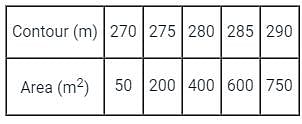
The areas enclosed by the contours in a lake are as follows:

The volume of water between the contours 270 m and 290 m by trapezoidal formula is _______.
|
19 videos|31 docs|35 tests
|
|
19 videos|31 docs|35 tests
|


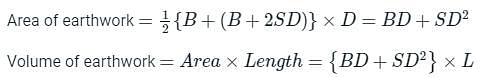
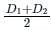

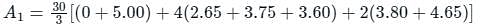
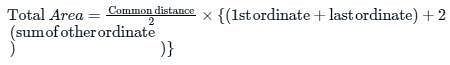




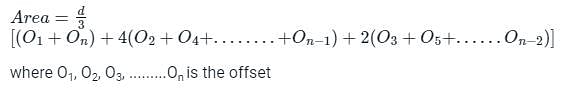
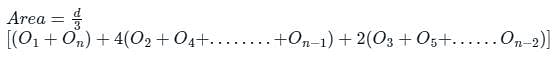

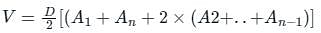

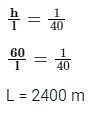

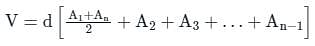

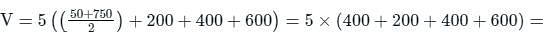 8000 m3
8000 m3














