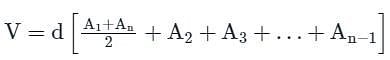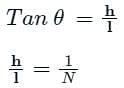Test: Measurements of Area & Volume - 2 - Civil Engineering (CE) MCQ
10 Questions MCQ Test Geomatics Engineering (Surveying) - Test: Measurements of Area & Volume - 2
Calculate the area in square meters enclosed between the survey line, the irregular boundary line, and the first and last offsets by Simpson's rule. The perpendicular offsets were taken at 20 m intervals from a survey line to an irregular boundary line: 2.35, 6.50, 5.40, 6.65, 7.85, 6.2, 2.35, 6.5, 5.65
Which of the following is an application of simpson’s rule?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Calculate the volume of the third section with areas of 76.32 m2 and 24.56 m2, separated by 4 m.
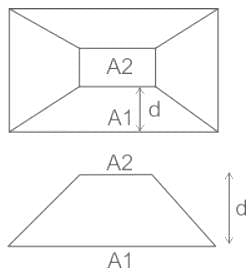
The areas enclosed by the contours in a lake are as follows:
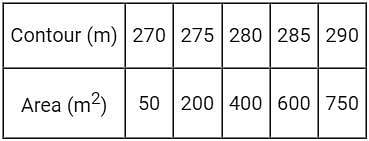
The volume of water between the contours 270 m and 290 m by trapezoidal formula is _______.
The Simpson’s rule for determination of areas is used when the number of offsets are:
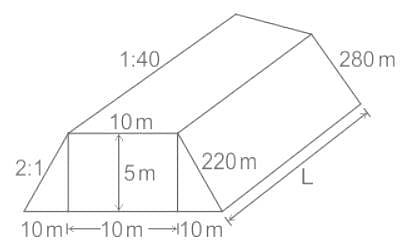
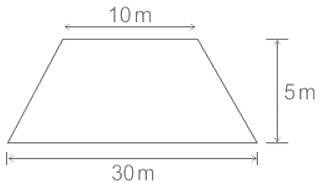
A road embankment 10 m wide at the formation level with side slopes 2:1 and with an average height of 5 m is constructed with an average gradient of 1:40 from the contour 220 m to 280 m. Find the volume of earthwork.
The alternate name of Trapezoidal Formula's is______.
All the dimensions of the embankment were measured with 20 m chain and the volume was calculated as 368.85 cubic meter. It was then found that the chain was 10 cm too long. Find the true volume of embankment?
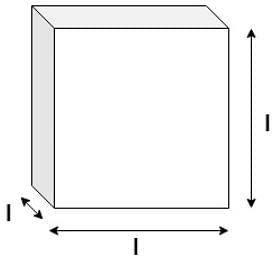
A cube of side equal to 20 cm is open from the top. Its total surface area is __________ cm2.
Total surface area of a cube having sides l is given by __________.
|
19 videos|31 docs|35 tests
|
|
19 videos|31 docs|35 tests
|