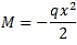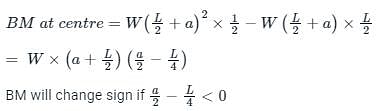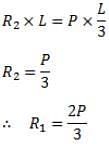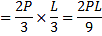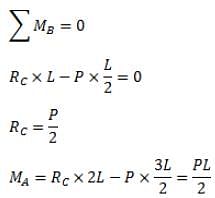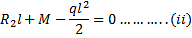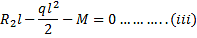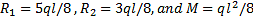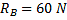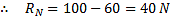Test: Bending Moment - Civil Engineering (CE) MCQ
10 Questions MCQ Test RCC & Prestressed Concrete - Test: Bending Moment
The shapes of the bending moment diagram for a uniform cantilever beam carrying a uniformly distributed load over its length is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
In a simply supported beam of span (L + 2a) with equal overhang (a) carries a uniformly distributed load over the whole length. Bending moment changes sign if -
A concentrated load P acts on a simply supported beam of span L at a distance L/3 from the left support. The bending moment at the point of application of the load is given by
At what height from the base of a pillar must the end of a rope of length l be fixed so that a man standing on the ground and pulling it at the other end may have the greatest tendency to overturn the pillar
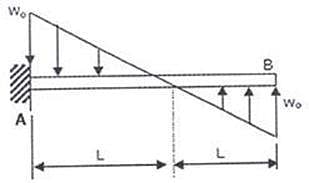
A cantilever beam carriers the anti symmetric load as shown, where w is the peak intensity of the distributed load. Qualitatively, the correct bending moment diagram for the beam is
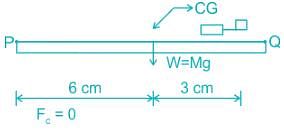
A mobile phone has a small motor with an eccentric mass used for vibrator mode. The location of the eccentric mass on motor with respect to center of gravity (CG) of the mobile and the rest of the dimensions of the mobile phone are shown. The mobile is kept on a flat horizontal surface.
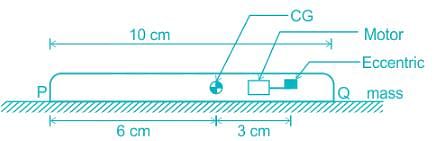
Given in addition that the eccentric mass = 2 grams, eccentricity = 2.19 mm, mass of the mobile = 90 grams, g = 9.81 m/s2. Uniform speed of the motor in RPM for which the mobile will get just lifted off the ground at the end Q is approximately.
A beam is made up of two identical bars AB and BC by hinging them together at B. the end A is built in (cantilevered) and the end C is simply supported. With the load P acting as shown, the bending moment at A is

A uniformly loaded propped cantilever beam and its free body diagram are shown below. The reaction are
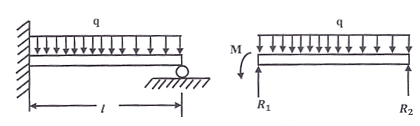
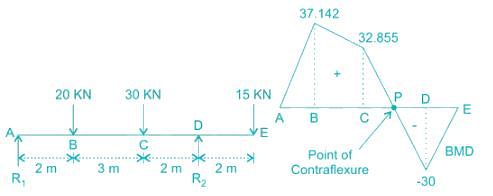
In a simply-supported beam loaded as shown below, the maximum bending moment is Nm is

|
13 videos|42 docs|34 tests
|
|
13 videos|42 docs|34 tests
|