Test: Relational Algebra - 2 - Computer Science Engineering (CSE) MCQ
10 Questions MCQ Test Database Management System (DBMS) - Test: Relational Algebra - 2
Assume the given tables Dance and Music.
Dance
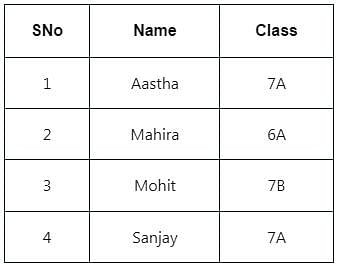
Music
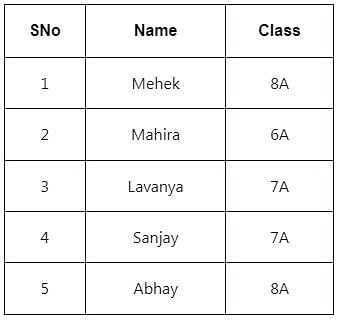
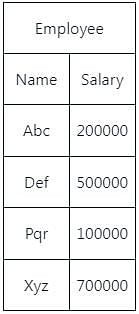
Which operation should be applied to the table to get the following output?

Music


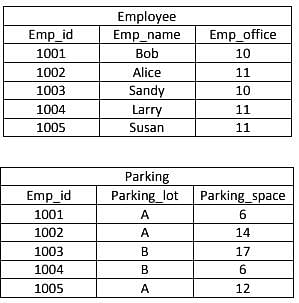
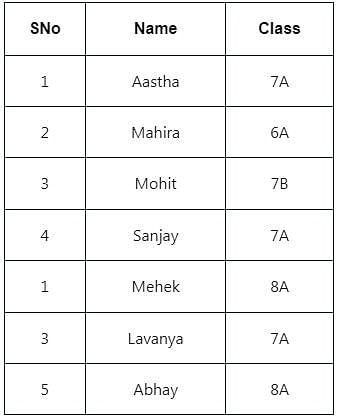
Consider the table given below.
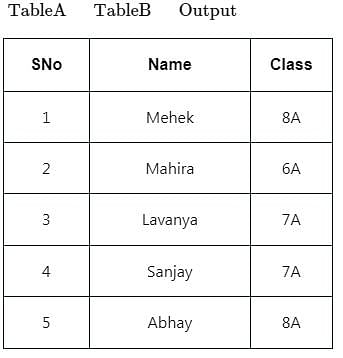
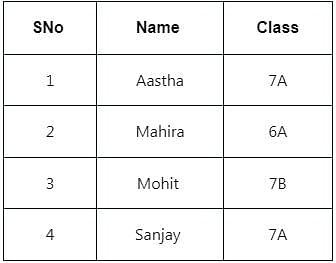
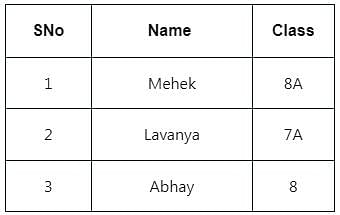
Identify the operation applied to the given tables to get the given output



| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If P and Q are predicates and P is the relational algebra expression, then which of the following equivalence are valid ?
Consider the relation schemas R(A, B, C, D) and S(D, E, F). What will be the degree of the resultant schema R * S, where star (*) symbol represents the natural join operation?
In a relational database model, cardinality of a relation means
Which of the following forms the complete set of Relational Algebra operations?
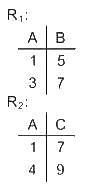
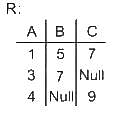
Consider two relations R1(A, B) with the tuples (1, 5), (3, 7) and R2(A, C) = (1, 7), (4, 9). Assume that R(A, B, C) is the full natural outer join of R1 and R2. Consider the following tuples of the form (A, B, C): a = (1, 5, null), b = (1, null, 7), c = (3, null, 9), d = (4, 7, null), e = (1, 5, 7), f = (3, 7, null), g = (4, null, 9). Which one of the following statements is correct?
Let R and S be two database relations. If cardinalities of R and S are 4 and 10, respectively, then what will be the number of tuples in R × S, where '×' represents cross product operation?
|
62 videos|66 docs|35 tests
|
|
62 videos|66 docs|35 tests
|