Test: Recursion- 3 - Computer Science Engineering (CSE) MCQ
20 Questions MCQ Test Question Bank for GATE Computer Science Engineering - Test: Recursion- 3
Consider the following recursive function fun(x, y). What is the value of fun(4, 3)
int fun(int x, int y)
{
if (x == 0)
return y;
return fun(x - 1, x + y);
int fun(int x, int y)
{
if (x == 0)
return y;
return fun(x - 1, x + y);
Predict output of following program
#include <stdio.h>
int fun(int n)
{
if (n == 4)
return n;
else return 2*fun(n+1);
}
int main()
{
printf("%d ", fun(2));
return 0;
#include <stdio.h>
int fun(int n)
{
if (n == 4)
return n;
else return 2*fun(n+1);
}
int main()
{
printf("%d ", fun(2));
return 0;
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
What does the following function do?
int fun(int x, int y)
{
if (y == 0) return 0;
return (x + fun(x, y-1));
int fun(int x, int y)
{
if (y == 0) return 0;
return (x + fun(x, y-1));
What does the following function print for n = 25?
void fun(int n)
{
if (n == 0)
return;
printf("%d", n%2);
fun(n/2);
Output of following program?
#include<stdio.h>
void print(int n)
{
if (n > 4000)
return;
printf("%d ", n);
print(2*n);
printf("%d ", n);
}
int main()
{
print(1000);
getchar();
return 0;
}
What does fun2() do in general?
int fun(int x, int y)
{
if (y == 0) return 0;
return (x + fun(x, y-1));
}
int fun2(int a, int b)
{
if (b == 0) return 1;
return fun(a, fun2(a, b-1));
}
Predict the output of following program
#include <stdio.h>
int f(int n)
{
if(n <= 1)
return 1;
if(n%2 == 0)
return f(n/2);
return f(n/2) + f(n/2+1);
}
int main()
{
printf("%d", f(11));
return 0;
}
Find the number of elements in the following array.
float f [6] [4] [2];
What does the following function do?
int fun(unsigned int n)
{
if (n == 0 || n == 1)
return n;
if (n%3 != 0)
return 0;
return fun(n/3);
}
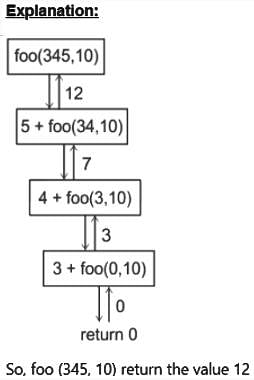
Consider the following recursive C function that takes two arguments
unsigned int foo(unsigned int n, unsigned int r) {
if (n > 0) return (n%r) + foo (n/r, r));
else return 0;
}
What is the return value of the function foo when it is called as foo(345, 10) ?
Consider the same recursive C function that takes two arguments
unsigned int foo(unsigned int n, unsigned int r) {
if (n > 0) return (n%r + foo (n/r, r ));
else return 0;
}
What is the return value of the function foo when it is called as foo(513, 2)?
Output of following program?
#include <stdio.h>
int fun(int n, int *f_p)
{
int t, f;
if (n <= 1)
{
*f_p = 1;
return 1;
}
t = fun(n- 1,f_p);
f = t+ * f_p;
*f_p = t;
return f;
}
int main()
{
int x = 15;
printf (" %d n", fun(5, &x));
return 0;
}
#include<stdio.h>
int f(int *a, int n)
{
if(n <= 0) return 0;
else if(*a % 2 == 0) return *a + f(a+1, n-1);
else return *a - f(a+1, n-1);
}
int main()
{
int a[] = {12, 7, 13, 4, 11, 6};
printf("%d", f(a, 6));
getchar();
return 0;
}
Consider the C function given below.
int f(int j)
{
static int i = 50;
int k;
if (i == j)
{
printf(“something”);
k = f(i);
return 0;
}
else return 0;
}
Which one of the following is TRUE?
Which of the following statements are CORRECT?
1) Static allocation of all data areas by a compiler makes it impossible to implement recursion.
2) Automatic garbage collection is essential to implement recursion
3) Dynamic allocation of activation records is essential to implement recursion
4) Both heap and stack are essential to implement recursion
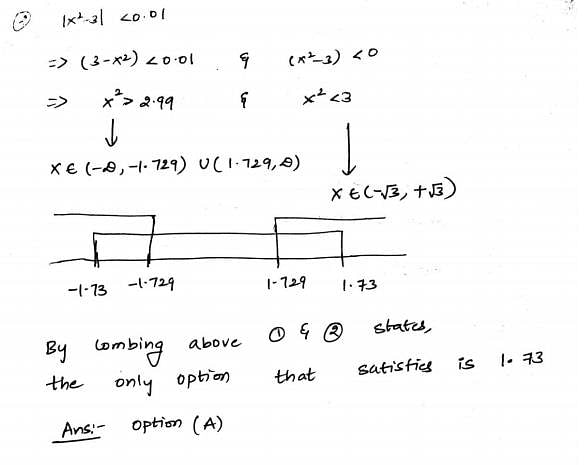
Consider the following function
double f(double x){
if (abs(x*x - 3) < 0.01) return x;
else return f(x/2 + 1.5/x);
}
Give a value q (to 2 decimals) such that f(q) will return q:_____.
Consider the following C function.
int fun (int n)
{
int x=1, k;
if (n==1) return x;
for (k=1; k<n; ++k)
x = x + fun(k) * fun(n – k);
return x;
}
The return value of fun(5) is __________.
Consider the following recursive C function. If get(6) function is being called in main() then how many times will the get() function be invoked before returning to the main()?
void get (int n)
{
if (n < 1) return;
get(n-1);
get(n-3);
printf("%d", n);
}
The function f is defined as follows:
int f (int n) {
if (n <= 1) return 1;
else if (n % 2 == 0) return f(n/2);
else return f(3n - 1);
}
Assuming that arbitrarily large integers can be passed as a parameter to the function, consider the following statements.
1. The function f terminates for finitely many different values of n ≥ 1.
ii. The function f terminates for infinitely many different values of n ≥ 1.
iii. The function f does not terminate for finitely many different values of n ≥ 1.
iv. The function f does not terminate for infinitely many different values of n ≥ 1.
Which one of the following options is true of the above?
|
63 videos|7 docs|165 tests
|
|
63 videos|7 docs|165 tests
|