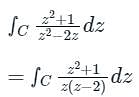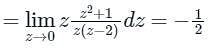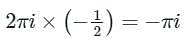Test: Cauchy’s Integral Theorem - 1 - Civil Engineering (CE) MCQ
10 Questions MCQ Test Engineering Mathematics - Test: Cauchy’s Integral Theorem - 1
The values of the integral 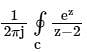 along a closed contour c in anti-clockwise direction for
along a closed contour c in anti-clockwise direction for
(i) the point z0 = 2 inside the contour c, and
(ii) the point z0 = 2 outside the contour c, respectively, are
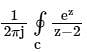 along a closed contour c in anti-clockwise direction for
along a closed contour c in anti-clockwise direction for(i) the point z0 = 2 inside the contour c, and
(ii) the point z0 = 2 outside the contour c, respectively, are
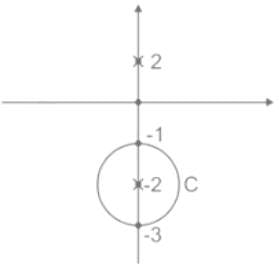
The value of the integral 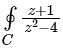 dz in counter clockwise direction around a circle C of radius 1 with center at the point z = −2 is
dz in counter clockwise direction around a circle C of radius 1 with center at the point z = −2 is
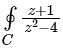 dz in counter clockwise direction around a circle C of radius 1 with center at the point z = −2 is
dz in counter clockwise direction around a circle C of radius 1 with center at the point z = −2 isIf C is a circle of radius r with center z0, in the complex z-plane and if n is a non-zero integer, then equals
equals
 equals
equalsIf f(z) is analytic in a simply connected domain D, then for every closed path C and D
The value of the contour integral in the complex plane

along the contour |z| = 3, taken counterclockwise is
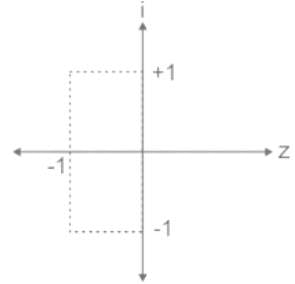
Evaluate  where C is the rectangular region defined by x = 0, x = 4, y = -1 and y = 1
where C is the rectangular region defined by x = 0, x = 4, y = -1 and y = 1
The value of the integral
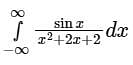
evaluated using contour integration and the residue theorem is
Let C represent the unit circle centered at origin in the complex plane, and complex variable, z = x + iy. The value of the contour integral 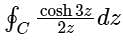 (where integration is taken counter clockwise) is
(where integration is taken counter clockwise) is
The value of the following complex integral, with C representing the unit circle centered at origin in the counterclockwise sense, is: 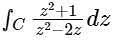
|
65 videos|120 docs|94 tests
|


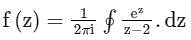 The singular point is at z = 2.
The singular point is at z = 2.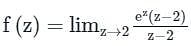
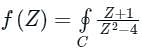


 we consider f(z)/(z-a) to be analytic at all points within C except at z=a.
we consider f(z)/(z-a) to be analytic at all points within C except at z=a.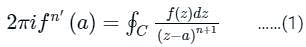
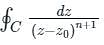
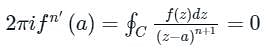
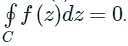
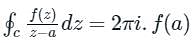
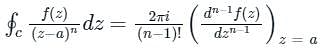
 is given by
is given by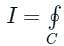 Cf(z)dz = 2π i × {Sum of residue of poles in side or onC}
Cf(z)dz = 2π i × {Sum of residue of poles in side or onC}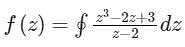
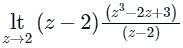 = 23 − 2(2) + 3 = 7
= 23 − 2(2) + 3 = 7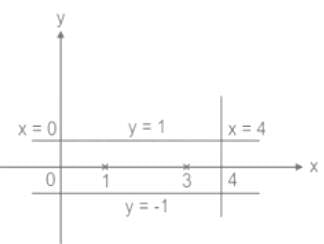
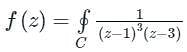
 f (z)dz = 2πi [sum of the residues at the poles in side ′C′]
f (z)dz = 2πi [sum of the residues at the poles in side ′C′]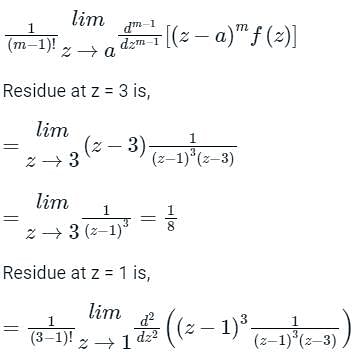
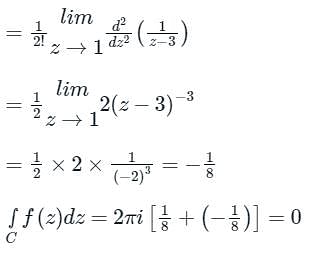
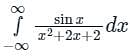
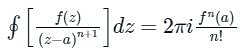
 = Sum of Residue at Pole or singularity with in the region
= Sum of Residue at Pole or singularity with in the region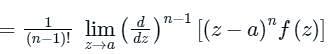
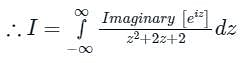
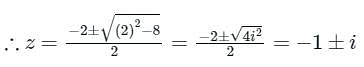
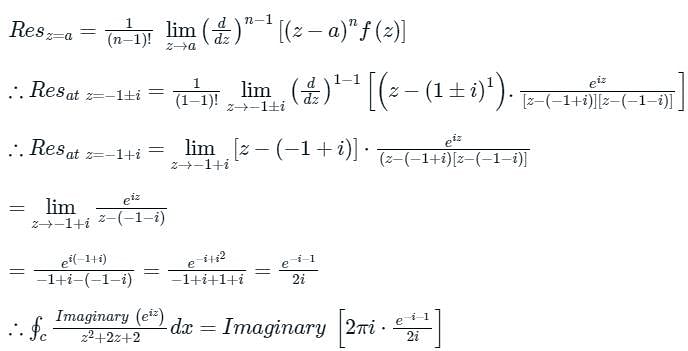

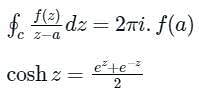
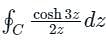 where C represents unit circle i.e. radius is unity.
where C represents unit circle i.e. radius is unity.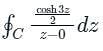
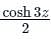 and a = 0.
and a = 0.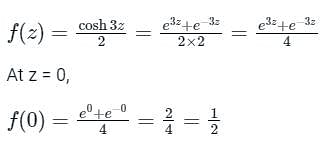
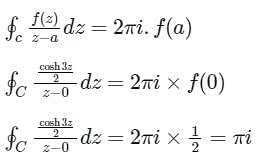
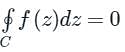
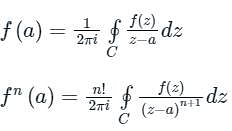
 f(z)dz = 2πi × [sum of residues at the singualr points with in C]
f(z)dz = 2πi × [sum of residues at the singualr points with in C]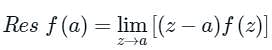 2. If f(z) has a pole of order n at z = a, then
2. If f(z) has a pole of order n at z = a, then