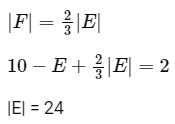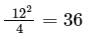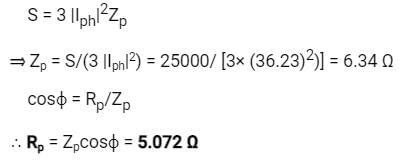Test: Graph Theory - Computer Science Engineering (CSE) MCQ
10 Questions MCQ Test - Test: Graph Theory
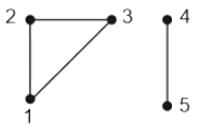
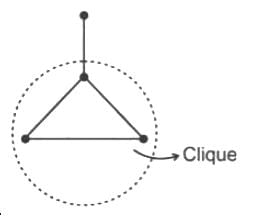
Which of the following properties of the circuits of a graph are correct?
- The minimum number of branches possible in a circuit will be equal to the number of elements in a circuit.
- There are exactly two paths between any pair of vertices in a circuit.
- There are at least two branches in a circuit.
Select the correct answer using the code given below.
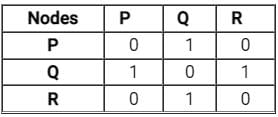
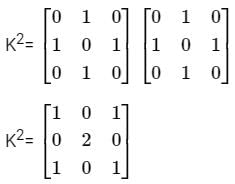
Which of the properties hold for the adjacency matrix A of a simple undirected unweighted graph having n vertices?
Let G be a connected planar graph with 10 vertices. If the number of edges on each face is three, then the number of edges in G is ________.
Let G = (V, E) be a directed graph where V is the set of vertices and E the set of edges. Then which one of the following graphs has the same strongly connected components as G?
The minimum number of colours that is sufficient to vertex-colour any planar graph is_______.
In a connected graph, a bridge is an edge whose removal disconnects a graph. Which one of the following statements is true?
The maximum number of edges in a bipartite graph on 12 vertices is ________
A star connected network consumes a power of 20 kW with a power factor of 0.8. Calculate the value of resistance of each coil when a supply voltage of 230 volts and 50 Hz is supplied between two phases of the network.
A path is a particular subgraph consisting of an ordered sequence of branches having which of the following properties?
1. At all but two of its nodes, called internal nodes, there are incident exactly two branches of the subgraph.
2. At each of the remaining two nodes, called terminal nodes, there is incident exactly one branch of the subgraph.
Select the correct answer using the code given below.
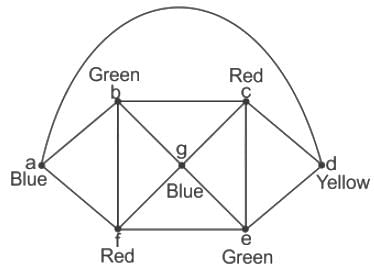
The following simple undirected graph is referred to as the Peterson graph.
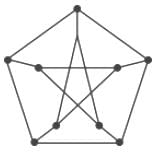
Which of the following statements is/are TRUE?